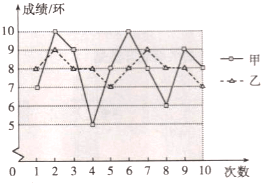
题目内容
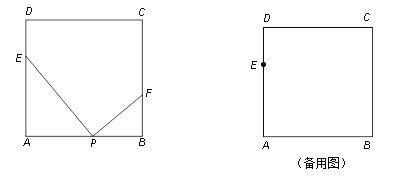
【题目】如图,在正方形ABCD中,AB=4cm,点E为AC边上一点,且AE=3cm,动点P从点A出发,以1cm/s的速度沿线段AB向终点B运动,运动时间为x s.作∠EPF=90°,与边BC相交于点F.设BF长为ycm.
(1)当x= s时,EP=PF;
(2)求在点P运动过程中,y与x之间的函数关系式;
(3)点F运动路程的长是 cm.
【答案】(1)当x=1s时,EP=PF;(2)y=﹣![]() x2+
x2+![]() x;(3)点F运动路程是
x;(3)点F运动路程是![]() cm.
cm.
【解析】
(1)利用全等三角形的性质即可解决问题;
(2)利用相似三角形的性质,即可解决问题;
(3)两条二次函数的性质,求出y的最大值即可解决问题;
(1)∵四边形ABCD是正方形,∠EPF=90°,
∴∠A=∠B=90°,
∴∠APE+∠AEP=90°,∵∠APE+∠BPF=90°,
∴∠BPF=∠AEP,∵EP=PF,
∴△AEP≌△BPF,
∴AE=PB=3,
∴AP=AB﹣PB=1,
∴当x=1s时,EP=PF;
(2)∵∠EPF=90°,
∴∠EPA+∠BPF=90°
又∵∠EPA+∠AEP=90°,
∴∠AEP=∠BPF,
在△EAP与△PBF中,
∠AEP=∠BPF,∠EAP=∠PBF=90°,
∴△EAP∽△PBF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴y=﹣![]() x2+
x2+![]() x.
x.
(3)∵y=﹣![]() x2+
x2+![]() x=﹣
x=﹣![]() (x﹣2)2+
(x﹣2)2+![]() ,
,
∵﹣![]() <0,
<0,
∴y有最大值,最大值为![]() ,
,
∴点F运动路程是![]() cm.
cm.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目