��Ŀ����
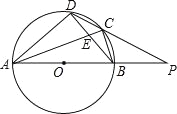
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У���D��ֱ��y=��x��һ�㣬��O��D�����Բ��O1�ֱ�x�ᡢy���ڵ�A��B��
��1����A����12��0����B��0����5��ʱ����O1�����ꣻ

��2���ڣ�1���������£�����A����O1��������BD���ӳ����ཻ�ڵ�C�����C�����ꣻ

��3������D�ĺ�����Ϊ![]() ����IΪ��ABO�����ģ�IE��AB��E������O��D����ġ�O1�Ĵ�С�����仯ʱ������ۣ�AE��BE��ֵ�Ƿ����仯�������䣬�������ֵ�����仯��������仯��Χ��
����IΪ��ABO�����ģ�IE��AB��E������O��D����ġ�O1�Ĵ�С�����仯ʱ������ۣ�AE��BE��ֵ�Ƿ����仯�������䣬�������ֵ�����仯��������仯��Χ��

���𰸡���1��O1����6����2.5������2��C����7��12������3��������.
��������
��1������AB������O1��O1K��OA�ڵ�K���ɡ�AOB=90������֪��AB��Բ��O1����֪��A����B�����꣬O1A=O1B����O1K=![]() OB��OK=
OB��OK=![]() OA���Ӷ��ɽ���O1�����������
OA���Ӷ��ɽ���O1�����������
��2��֤��ACH�ա�BAO����CH=OA��OH=AO-OB���Ӷ��ɽ���C�����������
��3���������ߣ���DN��X����N��DM��Y����M����֪���ı���DMONΪ�����Σ�ͨ��֤����ADN�ա�BDM����AN=BM����AE-BEAG-BF=��OA-OG��-��OB-OF��=OA-OB=��AN+OG��-��AN-MO��=OG+OM=7Ϊ��ֵ��
��1������AB������O1��O1K��OA�ڵ�K��
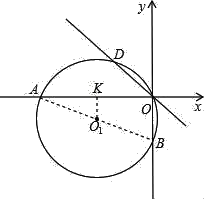
�ߡ�AOB=90�㣬
��AB����Բ��O1��
��A����12��0����B��0����5����O1K��O1A��O1A=O1B��
��O1K=![]() OB=2.5��OK=
OB=2.5��OK=![]() OA=
OA=![]() ��12=6��
��12=6��
��O1����6����2.5����
��2������C��CH��x���ڵ�H������AD��AB��

��AC��O1������
���CAB=90�㣬
��ֱ��OD����ʽΪy=��x��
���AOD=��ABD=45�㣬
���ABCΪ����ֱ�������Σ�
��AC=AB��
��ACΪ��O1�����ߣ�
���CAH=��ABO��
�ߡ�CHA=��AOB=90�㣬AC=AB��
���ACH�ա�BAO��
��CH=OA=12��OH=AO��OB=12��5=7��
���C����7��12����
��3��D��ֱ��y=��x��һ�㣬��DN��X����N��DM��Y����M��

DM=DN=NO=MO��G��F�ֱ�����X�ᡢY����е㣬��AE=AG��BE=BF��IG=OG=OF=IF��
�ߡ�ADN+��NDB=90�㣬��BDM+��NDB=90��
���ADN=��BDM��
�ߡ�ADN=��BDM��ND=DM����AND=��BMD=90��
���ADN�ա�BDM��
��AN=BM��
��AE��BE=AG��BF��=��OA��OG������OB��OF��=OA��OB=��AN+ON������AN��MO��=ON+OM=![]() =7��
=7��