题目内容
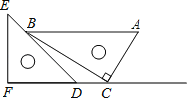
【题目】△ABC中,BC=12, 高AD=8,矩形EFGH的一边GH在BC上,顶点E、F分别在AB、AC上,AD与EF交于点M.
(1)求证:![]() ;
;
(2)矩形EFGH可以为正方形吗?若能,请求出正方形的面积,若不能,请说明理由;
(3)设EF=x, EH=y,设矩形EFGH的面积为S,求S与x之间的函数表达式,并求出S的最值.
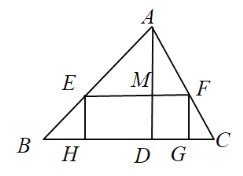
【答案】(1)见解析;(2)能,SEHGF=![]() ;(3)S=-
;(3)S=-![]() x2+8x,当x=6时S最大=24
x2+8x,当x=6时S最大=24
【解析】
(1)先判断出AM是△AEF的高,再判断出△AEF∽△ABC,即可得出结论;
(2)假设EFGH为正方形设EF=m,则AM=8-m,列出方程![]() 求出m的值即可得出答案;
求出m的值即可得出答案;
(3)先判断出四边形EMDG是矩形,得出DM=EH,进而表示出AM=8﹣y,借助(1)的结论即可得出结论;由矩形的面积公式得出函数关系式,即可得出结论.
(1)证明:∵矩形EFGH
∴EF∥BC
∵AD⊥BC
∴AD⊥EF
又∵△AEF∽△ABC
∴![]()
(2)能,解:假设EFGH为正方形设EF=m
∴AM=8-m
∴![]()
∴m=![]()
∴假设成立SEHGF=![]()
(3)∵EH=y
∴AM=8-y
∵![]()
∴![]()
∴y=8-![]() x
x
∵S=xy
∴S=x(8-![]() x)
x)
∴S=-![]() x2+8x=-
x2+8x=-![]() (x-6)2+24
(x-6)2+24
∴a=-![]() <0、
<0、
∴当x=6时S最大=24

练习册系列答案
相关题目