题目内容
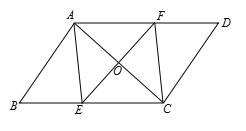
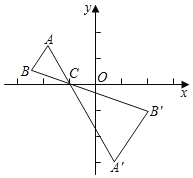
【题目】我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知∠A=90°, BD=4,CF=6, 则AO的长是 ( )

A.![]() B.
B.![]() C.
C.![]() D.4
D.4
【答案】B
【解析】
设正方形ADOF的边长为x,由题意可得BC的长,然后在直角△ACB中,利用勾股定理可建立关于x的方程,解方程即可求出x,进一步即可求出AO的长.
解:如图,设正方形ADOF的边长为x,
由题意得:BE=BD=4,CE=CF=6,
∴BC=BE+CE=10,
在Rt△ABC中,由勾股定理,得AC2+AB2=BC2,
即(6+x)2+(x+4)2=102,
整理得,x2+10x﹣24=0,
解得:x=2或x=﹣12(舍去),
即正方形ADOF的边长AD=2,
所以![]() .
.
故选:B.

【题目】为了了解某区九年级数学教学质量检测情况,进行了抽样调查,其过程如下,请补全表一、表二中的空白,并回答提出的问题.
收集数据:随机抽取甲、乙两所学校中各自取20名学生的数学成绩进行分析
甲:91 89 77 86 71 31 97 93 72 91 81 92 85 85 95 88 88 90 44 91
乙:84 93 66 69 76 87 77 82 85 88 90 88 67 88 91 96 68 97 59 88
整理数据:表一
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 | 0 | 0 | 1 | 2 | 8 | 5 |
分析数据:表二
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 | 88 | 91 | 268.43 |
乙 | 81.95 | 86 | 115.25 |
得出结论:
(1)若甲学校有400名九年级学生,估计这次考试成绩80分(包含80分)以上人数为 .
(2)可以推断出 (填:甲或乙)学校学生的数学水平较高,理由是 (至少从两个不同角度说明推断的合理性).