题目内容
【题目】小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°=![]() +
+![]() =1.
=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°-α)=1.
(1)当α=30°时,验证sin2α+sin2(90°-α)=1是否成立;
(2)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
【答案】(1)证明见解析;(2)成立,证明见解析
【解析】试题(1)将α=30°代入求值即可;(2)设∠A=α,∠B=90°-α,将∠A、∠B便可以是一个直角三角形的两个角,在直角三角形中利用正弦函数的定义及勾股定理即可验证.
解:(1)当α=30°时,sin2α+sin2(90°-α)=sin230°+sin260°=(![]() )2+(
)2+(![]() )2=
)2=![]() +
+![]() =1.
=1.
(2)小明的猜想成立,证明如下:
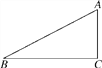
如图,在△ABC中,∠C=90°,设∠A=α,则∠B=90°-α,
∴sin2α+sin2(90°-α)=(![]() )2+(
)2+(![]() )2=
)2=![]() =
=![]() =1.
=1.
故猜想成立.

练习册系列答案
相关题目