Question

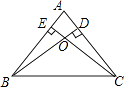
【题目】已知：如图，AM为⊙O的切线，A为切点，过⊙O上一点B作BD⊥AM于点D，BD交⊙O于点C，OC平分∠AOB．
（1）求∠AOB的度数；
（2）当⊙O的半径为2cm，求CD的长．

Answer 1

【答案】
（1）解：∵AM为圆O的切线，

∴OA⊥AM，

∵BD⊥AM，

∴∠OAD=∠BDM=90°，

∴OA∥BD，

∴∠AOC=∠OCB，

∵OB=OC，

∴∠OBC=∠OCB，

∵OC平分∠AOB，

∴∠AOC=∠BOC，

∴∠BOC=∠OCB=∠OBC=60°，

∴∠AOB=120°

（2）解：过点O作OE⊥BD于点E，

∵∠BOC=∠OCB=∠OBC=60°，

∴△OBC是等边三角形，

∴BE=EC=1，

∵∠OED=∠EDA=∠OAD=90°，

∴四边形OADE是矩形，

∴DE=OA=2，

∴EC=DC=1．

【解析】（1）由AM为圆O的切线，利用切线的性质得到OA与AM垂直，再由BD与AM垂直，得到OA与BD平行，利用两直线平行内错角相等得到一对角相等，再由OC为角平分线得到一对角相等，以及OB=OC，利用等边对等角得到一对角相等，等量代换得到∠BOC=∠OBC=∠OCB=60°，即可得出答案；（2）过点O作OE⊥BD于点E，进而得出四边形OADE是矩形，得出DC的长即可．
【考点精析】认真审题，首先需要了解切线的性质定理(切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)．