题目内容
【题目】如图,已知菱形ABCD的边长2,∠A=60°,点E、F分别在边AB、AD上,若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF= . 
【答案】![]()
【解析】解:延长CD,过点F作FM⊥CD于点M,连接GB、BD,作FH⊥AE交于点H,如图所示: ∵∠A=60°,四边形ABCD是菱形,
∴∠MDF=60°,
∴∠MFD=30°,
设MD=x,则DF=2x,FM= ![]() x,
x,
∵DG=1,∴MG=x+1,
∴(x+1)2+( ![]() x)2=(2﹣2x)2 ,
x)2=(2﹣2x)2 ,
解得:x=0.3,
∴DF=0.6,AF=1.4,
∴AH= ![]() AF=0.7,FH=AFsin∠A=1.4×
AF=0.7,FH=AFsin∠A=1.4× ![]() =
= ![]() ,
,
∵CD=BC,∠C=60°,
∴△DCB是等边三角形,
∵G是CD的中点,
∴BG⊥CD,
∵BC=2,GC=1,
∴BG= ![]() ,
,
设BE=y,则GE=2﹣y,
∴( ![]() )2+y2=(2﹣y)2 ,
)2+y2=(2﹣y)2 ,
解得:y=0.25,
∴AE=1.75,
∴EH=AE﹣AH=1.75﹣0.7=1.05,
∴EF= ![]() =
= ![]() =
= ![]() .
.
故答案为: ![]() .
.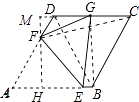
延长CD,过点F作FM⊥CD于点M,连接GB、BD,作FH⊥AE交于点H,由菱形的性质和已知条件得出∠MFD=30°,设MD=x,则DF=2x,FM= ![]() x,得出MG=x+1,由勾股定理得出(x+1)2+(
x,得出MG=x+1,由勾股定理得出(x+1)2+( ![]() x)2=(2﹣2x)2 , 解方程得出DF=0.6,AF=1.4,求出AH=
x)2=(2﹣2x)2 , 解方程得出DF=0.6,AF=1.4,求出AH= ![]() AF=0.7,FH=
AF=0.7,FH= ![]() ,证明△DCB是等边三角形,得出BG⊥CD,由勾股定理求出BG=
,证明△DCB是等边三角形,得出BG⊥CD,由勾股定理求出BG= ![]() ,设BE=y,则GE=2﹣y,由勾股定理得出(
,设BE=y,则GE=2﹣y,由勾股定理得出( ![]() )2+y2=(2﹣y)2 , 解方程求出y=0.25,得出AE、EH,再由勾股定理求出EF即可.
)2+y2=(2﹣y)2 , 解方程求出y=0.25,得出AE、EH,再由勾股定理求出EF即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目





