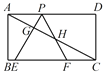
题目内容
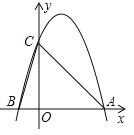
【题目】如图,线段AB、DC分别表示甲、乙两建筑物的高,AB⊥BC,DC⊥BC,从B点测得D点的仰角α为60°从A点测得D点的仰角β为30°,已知甲建筑物高AB=36米.
(1)求乙建筑物的高DC;
(2)求甲、乙两建筑物之间的距离BC
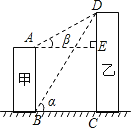
【答案】(1)乙建筑物的高DC为54米;(2)甲、乙两建筑物之间的距离BC为18![]() 米.
米.
【解析】
(1)过点A作AE⊥CD于点E,构造直角三角形△ADE和△DBC,设DE=x,在Rt△AED中 求得AE=![]() x,即可得BC=AE=
x,即可得BC=AE=![]() x.在Rt△DCB中,由tan∠DBC=tan60°=
x.在Rt△DCB中,由tan∠DBC=tan60°=![]() 可得方程
可得方程![]() ,解方程求得x的值,即可求得乙建筑物的高DC;(2)由BC=AE=
,解方程求得x的值,即可求得乙建筑物的高DC;(2)由BC=AE=![]() x,x=18即可求得BC的长.
x,x=18即可求得BC的长.
(1)过点A作AE⊥CD于点E.
根据题意,得∠DBC=∠α=60°,∠DAE=∠β=30°,AE=BC,EC=AB=36.
设DE=x,则DC=DE+EC=x+36.
在Rt△AED中,tan∠DAE=tan30°=![]() ,
,
∴AE=![]() x,∴BC=AE=
x,∴BC=AE=![]() x.
x.
在Rt△DCB中,tan∠DBC=tan60°=![]() ,
,
∴![]() ,
,
∴3x=x+36,
x=18,
经检验x=18是原方程的解.
∴DC=54米.
答:乙建筑物的高DC为54米;
(2)∵BC=AE=![]() x,x=18,
x,x=18,
∴BC=![]() ×18=18
×18=18![]() (米).
(米).
答:甲、乙两建筑物之间的距离BC为18![]() 米.
米.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目