题目内容
【题目】如图,在![]() 中,点
中,点![]() 为
为![]() 边的中点,以点
边的中点,以点![]() 为顶点的
为顶点的![]() 的两边分别与边
的两边分别与边![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,且
,且![]() 与
与![]() 互补.
互补.
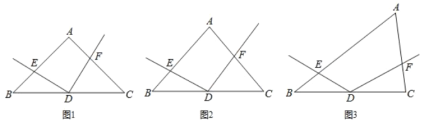
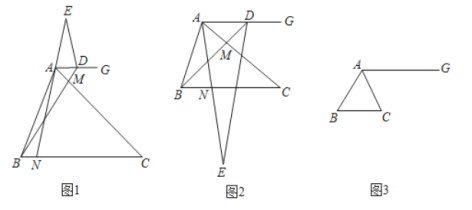
(1)如图1,若![]() ,且
,且![]() ,请直接写出:线段
,请直接写出:线段![]() 与
与![]() 的数量关系______;
的数量关系______;
(2)如图2,若![]() ,请直接写出:线段
,请直接写出:线段![]() 与
与![]() 的数量关系______;
的数量关系______;
(3)如图3,若![]() ,探索线段
,探索线段![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
【答案】(1)![]() ,理由见解析;(2)
,理由见解析;(2)![]() ,理由见解析;(3)结论
,理由见解析;(3)结论![]() ,理由见解析
,理由见解析
【解析】
(1)由等腰直角三角形的性质得出![]() ,∠B=∠DAF=45°,证出∠BED=∠AFD,证明△BED≌△AFD(AAS),即可得出结论;
,∠B=∠DAF=45°,证出∠BED=∠AFD,证明△BED≌△AFD(AAS),即可得出结论;
(2)过点D作DM⊥AB于M,作DN⊥AC于N,连接AD,由等腰直角三角形的性质得出AD平分∠BAC,得出DM=DN.证出∠MDE=∠NDF,证明△DEM≌△DFN(ASA),即可得出结论;
(3)过点D作DM⊥AB于M,作DN⊥AC于N,连接AD,由(2)得∠MDE=∠NDF,证明△DEM∽△DFN.得出![]() .证出S△ABD=S△ADC.得出
.证出S△ABD=S△ADC.得出![]() ,即可得出结论.
,即可得出结论.
(1)![]() ,理由如下:
,理由如下:
连接![]() .如图1所示:
.如图1所示:
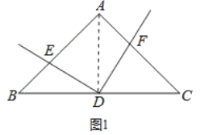
∵![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() .
.
故答案为:![]() ;
;
(2)![]() ,理由如下:
,理由如下:
过点![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,连接
,连接![]() .如图2所示:
.如图2所示:
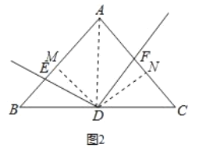
则![]() .
.
∵![]() ,点
,点![]() 为
为![]() 中点,
中点,
∴![]() 平分
平分![]() ,
,
∴![]() .
.
∵在四边形![]() 中,
中,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,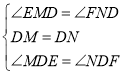 ,
,
∴![]() ,
,
∴![]() .
.
故答案为:![]() ;
;
(3)结论![]() ,理由如下:
,理由如下:
过点![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,连接
,连接![]() ,如图3所示:
,如图3所示:
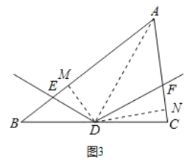
由(2)得![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵点![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() .
.

【题目】某校八年级学生在一次射击训练中,随机抽取10名学生的成绩如下表,请回答问题:
环数 | 6 | 7 | 8 | 9 |
人数 | 1 | 5 | 2 |
(1)填空:10名学生的射击成绩的众数是 ,中位数是 .
(2)求这10名学生的平均成绩.
(3)若9环(含9环)以上评为优秀射手,试估计全年级500名学生中有多少是优秀射手?
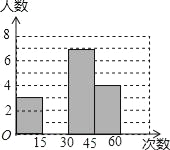
【题目】在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分 组 | 频数 | 频率 |
第一组(0≤x<15) | 3 | 0.15 |
第二组(15≤x<30) | 6 | a |
第三组(30≤x<45) | 7 | 0.35 |
第四组(45≤x<60) | b | 0.20 |
(1)频数分布表中a=_____,b=_____,并将统计图补充完整;
(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?
(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?