题目内容
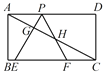
【题目】如图,已知矩形![]() ,在
,在![]() 上取两点
上取两点![]() 在
在![]() 左边),以
左边),以![]() 为边作等边三角形
为边作等边三角形![]() ,使顶点
,使顶点![]() 在
在![]() 上.
上.
(1)求△PEF的边长;
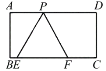
(2)若△PEF的边![]() 在线段
在线段![]() 上移动.
上移动.![]() 分别交
分别交![]() 于点
于点![]() .求证:
.求证:![]() .
.
【答案】(1)![]() 边长为
边长为![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)要求△PEF的边长,需构造直角三角形,那么就过P作PQ⊥BC于Q.利用∠PFQ的正弦值可求出PF,即△PEF的边长;
(2)利用∠1的正切值可求出∠1的度数,再由∠PFE=60°,可得出△HFC是等腰三角形,因此就有BE+EF+CF=BE+PH+2FH=3.再把其中FH用PH表示,化简即可.
(1)过P作PQ⊥BC于Q.
∵矩形ABCD中,∠B=90°,即AB⊥BC.
又∵AD∥BC,
∴PQ=AB![]() .
.
∵△PEF是等边三角形,
∴∠PFQ=60°.
在Rt△PQF中,PF![]() 2,
2,
∴△PEF的边长为2;
(2)在Rt△ABC中,AB![]() ,BC=3,
,BC=3,
∴AC![]() ,
,
∴tan∠1=![]() ,
,
∴∠1=30°.
∵△PEF是等边三角形,
∴∠PFE=60°,PF=EF=2.
∵∠PFE=∠1+∠4,
∴∠4=30°,
∴∠1=∠4,
∴FC=FH.
∵PH+FH=2,BE+FC=3﹣EF=3﹣2=1,
∴PH﹣BE=(PH+FH)-(BE+FC)=1.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目