题目内容
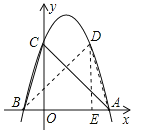
【题目】如图所示,二次函数![]() 的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图像上有一点D(x,y)(其中![]() ,
,![]() ),使
),使![]() ,求点D的坐标.
,求点D的坐标.
【答案】(1)3;(2)B(-1,0);(3)D(2,3).
【解析】
试题(1)由二次函数![]() 的图象与x轴的一个交点为A(3,0),利用待定系数法将点A的坐标代入函数解析式即可求得m的值;
的图象与x轴的一个交点为A(3,0),利用待定系数法将点A的坐标代入函数解析式即可求得m的值;
(2)根据(1)求得二次函数的解析式,然后将y=0代入函数解析式,即可求得点B的坐标;
(3)根据(2)中的函数解析式求得点C的坐标,由二次函数图象上有一点D(x,y)(其中x>0,y>0),可得点D在第一象限,又由![]() ,可知点D与点C的纵坐标相等,代入函数的解析式即可求得点D的坐标.
,可知点D与点C的纵坐标相等,代入函数的解析式即可求得点D的坐标.
试题解析:(1)∵二次函数![]() 的图象与x轴的一个交点为A(3,0),∴
的图象与x轴的一个交点为A(3,0),∴![]() ,解得:
,解得:![]() ;
;
(2)∵二次函数的解析式为:![]() ,∴当
,∴当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,![]() ,∴B(﹣1,0);
,∴B(﹣1,0);
(3)如图,连接BD、AD,过点D作DE⊥AB,∵当x=0时,y=3,∴C(0,3),若![]() ,∵D(x,y)(其中x>0,y>0),则可得OC=DE=3,∴当y=3时,
,∵D(x,y)(其中x>0,y>0),则可得OC=DE=3,∴当y=3时,![]() ,解得:x=0或x=2,∴点D的坐标为(2,3).
,解得:x=0或x=2,∴点D的坐标为(2,3).
另法:点D与点C关于x=1对称,故D(2,3).

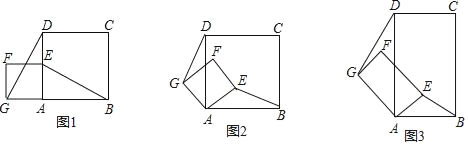
【题目】如图,△ABC、△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=![]() .将△BDE绕点B逆时针方向旋转后得△BD'E',当点E'恰好落在线段AD'上时,则CE'=_______.
.将△BDE绕点B逆时针方向旋转后得△BD'E',当点E'恰好落在线段AD'上时,则CE'=_______.
【题目】某快餐店共有10名员工,所有员工工资的情况如下表:
人员 | 店长 | 厨师甲 | 厨师乙 | 会计 | 服务员甲 | 服务员乙 | 勤杂工 |
人数 | 1 | 1 | 1 | 1 | 1 | 3 | 2 |
工资额 | 20000 | 7000 | 4000 | 2500 | 2200 | 1800 | 1200 |
请解答下列问题:
(1)餐厅所有员工的平均工资是 ;所有员工工资的中位数是 .
(2)用平均数还是用中位数描述该餐厅员工工资的一般水平比较恰当?
(3)去掉店长和厨师甲的工资后,其他员工的平均工资是多少?它是否也能反映该快餐店员工工资的一般水平?