Question

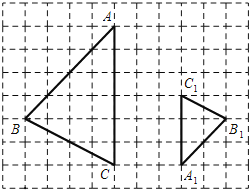
【题目】如图，在网格图中，与是位似图形．

若在网格上建立平面直角坐标系，使得点A的坐标为，点的坐标为，写出点B的坐标；

以点A为位似中心，在网格图中作，使和位似，且位似比为1：2；

在图上标出与的位似中心P，并写出点P的坐标，计算四边形ABCP的周长．

Answer 1

【答案】（1） ；（2）如图见解析（3） ； .

【解析】

（1）利用点A和C1的坐标画出直角坐标系，然后写出B点坐标；

（2）利用网格特点，根据位似的性质取AB的中点B2和AC的中点C2，则△AB2C2和△ABC位似，且位似比为 1：2；

（3）连结AA1、CC1、BB1，它们相交于点P，再写出P点坐标，然后利用勾股定理计算AB、BC、PC和AP的长，从而可得到四边形ABCP的周长．

（1）如图，点B的坐标为（﹣5，2）；

（2）如图，△AB2C2△为所作；

（3）如图，点P为所作，P点坐标为（1，2），AB==4，BC==2，PC==2，AP==2，所以四边形ABCP的周长=4+2+2+2=6+4．

故答案为：（﹣5，2），（1，2），6+4．