Question

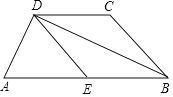
【题目】已知：如图，在梯形ABCD中，AB∥CD，BC＝CD，AD⊥BD，E为AB中点．

（1）求证：四边形BCDE是菱形．

（2）若AD＝6，BD＝8，求四边形BCDE的周长和面积．

Answer 1

【答案】（1）证明见解析；（2）周长：20；面积：24.

【解析】

（1）根据AD⊥BD，E为AB中点得到BE＝DE,再根据AB∥CD和BC＝CD，得到∠EDB＝∠EBD＝∠CDB＝∠CBD，证明△EBD≌△CBD,即可求解,（2）勾股定理求出AB=10,进而得到BE=5,求出周长,再求出S△ABD=24,利用S△DEB= S△ABD=12即可求出面积.

证明：（1）∵AD⊥BD，

∴△ABD是Rt△

∵E是AB的中点，

∴BE＝AB，DE＝AB （直角三角形斜边上的中线等于斜边的一半），

∴BE＝DE，

∴∠EDB＝∠EBD，

∵CB＝CD，

∴∠CDB＝∠CBD，

∵AB∥CD，

∴∠EBD＝∠CDB，

∴∠EDB＝∠EBD＝∠CDB＝∠CBD，

∵BD＝BD，

∴△EBD≌△CBD （ASA ），

∴BE＝BC，

∴CB＝CD＝BE＝DE，

∴菱形BCDE．（四边相等的四边形是菱形）

（2）∵△ABD是Rt△，AD＝6，BD＝8，

∴AB＝10（勾股定理），

∴S△ABD=，

∵E为AB中点，

∴S△DEB= S△ABD=12，

∴DE＝AB＝5，菱形BCDE的面积＝24，

∴菱形BCDE的周长＝20．