题目内容
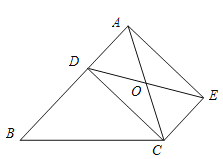
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

【答案】(1)证明见试题解析;(2)![]() .
.
【解析】试题分析:(1)先由旋转的性质得AE=AB,AF=AC,∠EAF=∠BAC,则∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,利用AB=AC可得AE=AF,于是根据旋转的定义,△AEB可由△AFC绕点A按顺时针方向旋转得到,然后根据旋转的性质得到BE=CD;
(2)由菱形的性质得到DE=AE=AC=AB=1,AC∥DE,根据等腰三角形的性质得∠AEB=∠ABE,根据平行线得性质得∠ABE=∠BAC=45°,所以∠AEB=∠ABE=45°,于是可判断△ABE为等腰直角三角形,所以BE=![]() AC=
AC=![]() ,于是利用BD=BE﹣DE求解.
,于是利用BD=BE﹣DE求解.
试题解析:(1)∵△AEF是由△ABC绕点A按顺时针方向旋转得到的,∴AE=AB,AF=AC,∠EAF=∠BAC,∴∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,∵AB=AC,∴AE=AF,∴△AEB可由△AFC绕点A按顺时针方向旋转得到,∴BE=CD;
(2)∵四边形ACDE为菱形,AB=AC=1,∴DE=AE=AC=AB=1,AC∥DE,∴∠AEB=∠ABE,∠ABE=∠BAC=45°,∴∠AEB=∠ABE=45°,∴△ABE为等腰直角三角形,∴BE=![]() AC=
AC=![]() ,∴BD=BE﹣DE=
,∴BD=BE﹣DE=![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目