��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��y=![]() x��
x��![]() ��x�ύ�ڵ�A��������A��������y=ax2��3x+c�ĶԳ�����x=
��x�ύ�ڵ�A��������A��������y=ax2��3x+c�ĶԳ�����x=![]() ��
��
��1���������ߵĽ���ʽ��
��2��ƽ��ֱ��l����ԭ��O���õ�ֱ��m����P��ֱ��m������һ�㣬PB��x���ڵ�B��PC��y���ڵ�C������E���߶�OB�ϣ���F���߶�OC���ӳ����ϣ�����PE��PF����PE=3PF����֤��PE��PF��
��3������2���еĵ�P����Ϊ��6��2������E��x���ϵĵ㣬��F��y���ϵĵ㣬��PE��PFʱ�����������Ƿ���ڵ�Q��ʹ�ı���PEQF�Ǿ��Σ�������ڣ��������Q�����꣬��������ڣ���˵�����ɣ�

���𰸡���1�������ߵĽ���ʽΪy=x2��3x��4����2��֤������������3����Q������Ϊ����2��6����2����6����
��������
��1������õ�A�����꣬Ȼ�����������߹���A���Գ�����x=![]() �г�����a��c�ķ�������⼴�ɣ�
�г�����a��c�ķ�������⼴�ɣ�
��2����P��3a��a������PC=3a��PB=a��Ȼ����֤����FPC=��EPB�����ͨ��������������֤�����ɣ�
��3����E��a��0����Ȼ���ú�a��ʽ�ӱ�ʾBE�ij����Ӷ��ɵõ�CF�ij������ǿɵõ���F�����꣬Ȼ�������е����깫ʽ�ɵõ�![]() ��
��![]() ���Ӷ�����õ�Q�����꣨�ú�a��ʽ�ӱ�ʾ���������Q��������������ߵĽ���ʽ���a��ֵ���ɣ�
���Ӷ�����õ�Q�����꣨�ú�a��ʽ�ӱ�ʾ���������Q��������������ߵĽ���ʽ���a��ֵ���ɣ�
��1����y=0ʱ��![]() �����x=4����A��4��0���������߹���A���Գ�����x=
�����x=4����A��4��0���������߹���A���Գ�����x=![]() ����
����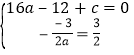 ��
��
���![]() �������ߵĽ���ʽΪy=x2��3x��4��
�������ߵĽ���ʽΪy=x2��3x��4��
��2����ƽ��ֱ��l����ԭ��O���õ�ֱ��m��
��ֱ��m�Ľ���ʽΪy=![]() x��
x��
�ߵ�P��ֱ��1������һ�㣬
����P��3a��a������PC=3a��PB=a��
�֡�PE=3PF��
��![]() ��
��
���FPC=��EPB��
�ߡ�CPE+��EPB=90�㣬
���FPC+��CPE=90�㣬
��FP��PE��
��3����ͼ��ʾ����E�ڵ�B�����ʱ����E��a��0������BE=6��a��
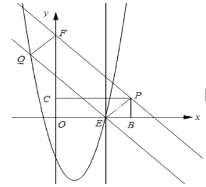
��CF=3BE=18��3a��
��OF=20��3a��
��F��0��20��3a����
��PEQF����
��![]() ��
��![]() ��
��
��Qx+6=0+a��Qy+2=20��3a+0��
��Qx=a��6��Qy=18��3a��
����Q��������������ߵĽ���ʽ�ã�18��3a=��a��6��2��3��a��6����4����ã�a=4��a=8����ȥ����
��Q����2��6����
����ͼ��ʾ������E�ڵ�B���Ҳ�ʱ����E��a��0������BE=a��6��
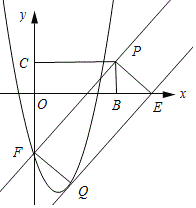
��CF=3BE=3a��18��
��OF=3a��20��
��F��0��20��3a����
��PEQF����
��![]() ��
��![]() ��
��
��Qx+6=0+a��Qy+2=20��3a+0��
��Qx=a��6��Qy=18��3a��
����Q��������������ߵĽ���ʽ�ã�18��3a=��a��6��2��3��a��6����4����ã�a=8��a=4����ȥ����
��Q��2����6����
������������Q����������2��6����2����6����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�




