题目内容
【题目】如图,已知ABCD中,AB=16,AD=10,sinA=![]() ,点M为AB边上一动点,过点M作MN⊥AB,交AD边于点N,将∠A沿直线MN翻折,点A落在线段AB上的点E处,当△CDE为直角三角形时,AM的长为_____.
,点M为AB边上一动点,过点M作MN⊥AB,交AD边于点N,将∠A沿直线MN翻折,点A落在线段AB上的点E处,当△CDE为直角三角形时,AM的长为_____.
【答案】4或8﹣![]()
【解析】
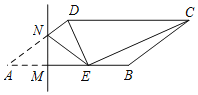
①当∠CDE=90°,如图1,根据折叠的性质得到MN⊥AB,AM=EM,得到AN=DN=![]() AD=5,设MN=3x,AN=5x=5,于是得到AM=4;②当∠DEC=90°,如图2,过D作DH⊥AB于H,根据相似三角形的性质得到
AD=5,设MN=3x,AN=5x=5,于是得到AM=4;②当∠DEC=90°,如图2,过D作DH⊥AB于H,根据相似三角形的性质得到![]() ,由sinA=
,由sinA=![]() ,AD=10,得到DH=6,AH=8,设HE=x,根据勾股定理求出x的值,继而求得AE的值,从而得到AM的值,即可得到结论.
,AD=10,得到DH=6,AH=8,设HE=x,根据勾股定理求出x的值,继而求得AE的值,从而得到AM的值,即可得到结论.
当△CDE为直角三角形时,
①当∠CDE=90°,如图1,
∵在ABCD中,AB∥CD,
∴DE⊥AB,
∵将∠A沿直线MN翻折,点A落在线段AB上的点E处,
∴MN⊥AB,AM=EM,
∴MN∥DE,
∴AN=DN=![]() AD=5,
AD=5,
∵sinA=![]() ,
,
∴设MN=3x,AN=5x=5,
∴MN=3,
∴AM=4;
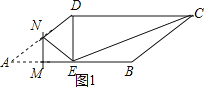
②当∠DEC=90°,如图2,
过D作DH⊥AB于H,
∵AB∥CD,
∴∠HDC=90°,
∴∠HDC+∠CDE=∠CDE+∠DCE=90°,
∴∠HDE=∠DCE,
∴△DHE∽△CED,
∴![]() ,
,
∵sinA=![]() ,AD=10,
,AD=10,
∴DH=6,
∴AH=8,
设HE=x,
∴DE=![]() ,
,
∵DH2+HE2=DE2,
∴62+x2=16x,
∴x=8﹣2![]() ,x=8+2
,x=8+2![]() (不合题意舍去),
(不合题意舍去),
∴AE=AH+HE=16﹣2![]() ,
,
∴AM=![]() AE=8﹣
AE=8﹣![]() ,
,
综上所述,AM的长为4或8﹣![]() ,
,
故答案为:4或8﹣![]() .
.


练习册系列答案
相关题目



