题目内容
已知关于x的方程(a-1)x2+2x+a-1=0.
(1)若该方程有一根为2,求a的值及方程的另一根;
(2)当a为何值时,方程仅有一个根?求出此时a的值及方程的根.
(1)若该方程有一根为2,求a的值及方程的另一根;
(2)当a为何值时,方程仅有一个根?求出此时a的值及方程的根.
考点:根的判别式,根与系数的关系
专题:
分析:(1)把x=2代入方程,求出a的值,再把a代入原方程,进一步解方程即可;
(2)分两种情况探讨:①当a=1时,为一元一次方程;②当a≠1时,利用b2-4ac=0求出a的值,再代入解方程即可.
(2)分两种情况探讨:①当a=1时,为一元一次方程;②当a≠1时,利用b2-4ac=0求出a的值,再代入解方程即可.
解答:解:(1)将x=2代入方程(a-1)x2+2x+a-1=0,
解得:a=
.
将a=
代入原方程得-
x2+2x-
=0,
解得:x1=
,x2=2.
∴a=
,方程的另一根为
.
(2)①当a=1时,方程为2x=0,
解得:x=0;
②当a≠1时,由b2-4ac=0得4-4(a-1)2=0,
解得:a=2或0.
当a=2时,原方程为:x2+2x+1=0,
解得:x1=x2=-1;
当a=0时,原方程为:-x2+2x-1=0,
解得:
=
=1.
解得:a=
| 1 |
| 5 |
将a=
| 1 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
解得:x1=
| 1 |
| 2 |
∴a=
| 1 |
| 5 |
| 1 |
| 2 |
(2)①当a=1时,方程为2x=0,
解得:x=0;
②当a≠1时,由b2-4ac=0得4-4(a-1)2=0,
解得:a=2或0.
当a=2时,原方程为:x2+2x+1=0,
解得:x1=x2=-1;
当a=0时,原方程为:-x2+2x-1=0,
解得:
| x | ′ 1 |
| x | ′ 2 |
点评:此题考查一元二次方程根的判别式,以及探讨方程有一根的两种情况:一元一次方程和一元二次方程有两个相等的实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,∠AOB=180°,OD是∠COB的平分线,OE是∠AOC的平分线,设∠BOD=α,则与α的余角相等的角是
如图,∠AOB=180°,OD是∠COB的平分线,OE是∠AOC的平分线,设∠BOD=α,则与α的余角相等的角是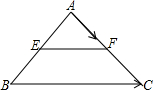 已知:如图,EF是△ABC的中位线,设
已知:如图,EF是△ABC的中位线,设 如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为r米,面积为S平方米.(注:π的近似值取3)
如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为r米,面积为S平方米.(注:π的近似值取3) 已知二次函数y=x2+bx+c的图象经过点(4,3),(3,0).
已知二次函数y=x2+bx+c的图象经过点(4,3),(3,0). 如图,AB为⊙O的直径,射线AP交⊙O于C点,∠PCO的平分线交⊙O于D点,过点D作DE⊥AP交AP于E点.
如图,AB为⊙O的直径,射线AP交⊙O于C点,∠PCO的平分线交⊙O于D点,过点D作DE⊥AP交AP于E点. 如图,在平行四边形ABCD中,E为CD上一点,联结AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF=
如图,在平行四边形ABCD中,E为CD上一点,联结AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF=