��Ŀ����
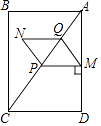
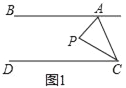
����Ŀ����ͼ��ʾ��ֱ��AC��BD������AB��ֱ��AC��BD���߶�AB��ƽ��ֳɢ١��ڡ��ۡ����ĸ����֣��涨�����ϸ��㲻�����κβ��֣�������P����ij������ʱ������PA��PB�����ɡ�PAC����APB����PBD�����ǣ���ʾ���й����˵�������غϵ���������ɵĽ���0�㣩��
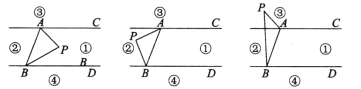
��1��������P���ڵڢٲ���ʱ����֤����APB����PAC����PBD��
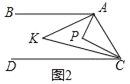
��2��������P���ڵڢڲ���ʱ����APB����PAC����PBD�Ƿ������ֱ�ӻش������������
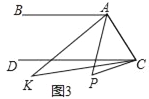
��3��������P�ڵڢ۲���ʱ��ȫ��̽����PAC����APB����PBD֮��Ĺ�ϵ����д������P�ľ���λ�ú���Ӧ�Ľ��ۣ�ѡ������һ�ֽ��ۼ���֤����
���𰸡���1��֤������������2������������3��֤��������
��������
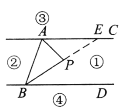
��1����ͼ���ӳ�BP��ֱ��AC�ڵ�E����AC��BD����֪��PEA=��PBD���ɡ�APB=��PAE+��PEA����֪��APB=��PAC+��PBD��
��2������P��AC��ƽ���ߣ�����ƽ���ߵ����ʽ��
��3������P�IJ�ͬλ�ã��֢ٵ�����P������BA���Ҳ�ʱ���ڵ�����P������BA��ʱ���۵�����P������BA�����ʱ������������ۣ�
�⣺��1����ͼ��ʾ���ӳ�BP��ֱ��AC�ڵ�E��
��ΪAC��BD�����ԡ�PEA����PBD��
��Ϊ��APB����PAE+��PEA�����ԡ�APB����PAC+��PBD��
��2���������� ��
��P��PM��AC��
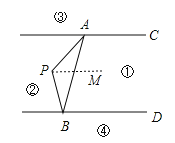
��AC��BD��
��AC��PM��BD��
���PAC+��APM=180������PBD+��BPM=180����
���APB+��PAC+��PBD=360�����������Ƴ���APB=��PAC+��PBD��
�ʲ�������
��3���ٵ�����P������BA���Ҳ�ʱ�������ǡ�PBD=��PAC+��APB��
�ڵ�����P������BA��ʱ�������ǡ�PBD����PAC+��APB�����PAC����PBD+��APB���APB��0�㣬��PAC=��PBD����дһ�����ɣ���
�۵�����P������BA�����ʱ�������ǡ�PAC=��APB+��PBD
ѡ���֤����
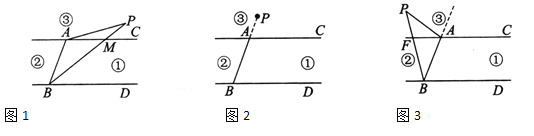
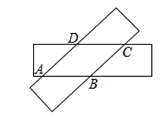
��ͼ1��ʾ������PA������PB��AC�ڵ�M��
��ΪAC��BD�����ԡ�PMC����PBD��
����Ϊ��PMC����PAMʮ��APM�����ԡ�PBD����PAC+��APB��
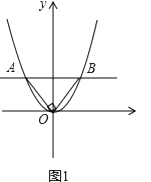
ѡ���֤������ͼ2��ʾ����Ϊ��P������BA�ϣ����ԡ�APB��0�㣮
��ΪAC��BD�����ԡ�PBD����PAC��
���ԡ�PBD����PAC����APB���PAC=��PBD+��APB���APB��0�㣬��PAC=��PBD��
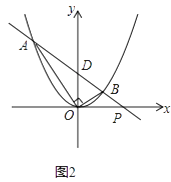
ѡ���֤�������ͼ3��ʾ������PA������PB��AC�ڵ�F��
��ΪAC��BD�����ԡ�PFA����PBD��
��Ϊ��PAC����APF+��PFA�����ԡ�PAC����APF+��PBD��
���ԡ�PAC=��APB+��PBD��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��Ϊ���Ϳ�����Ⱦ�������ɺ�����˾����ȫ���������ܻ�����ȼ�����������ƻ�����A�ͺ�B�����ֹ�������10��������ÿ̨�ļ۸����ؿ��������
A�� | B�� | |
�۸���Ԫ/̨�� | a | b |
���ؿ���������/�꣩ | 60 | 100 |
������A������1����B������2��������400��Ԫ��������A������2����B������1��������350��Ԫ��
��1����a��b��ֵ��
��2������ù�˾����A�ͺ�B���������ܷ��ò�����1200��Ԫ����ȷ����10���������ڸ���·������ؿ��ܺͲ�����680���˴Σ��������һ��������ʹ�ù����ܷ������٣�