��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У���֪A��B��������y=ax2��a��0����������ͬ�ĵ㣬����A�ڵڶ����ޣ�B�ڵ�һ���ޣ�
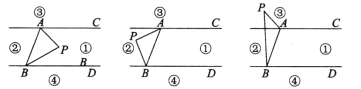
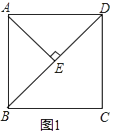
��1����ͼ1��ʾ����ֱ��AB��x��ƽ�У���AOB=90�㣬��AB=2ʱ����������ߵĽ���ʽ��A��B����ĺ�����ij˻���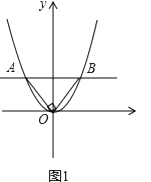
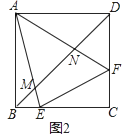
��2����ͼ2��ʾ���ڣ�1������õ��������ϣ���ֱ��AB��x�ƽ�У���AOB��Ϊ90��ʱ����֤��A��B���������ij˻���һ����ֵ��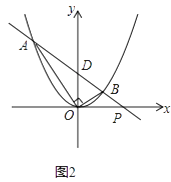
��3���ڣ�2���������£����ֱ��AB��x�ᡢy��ֱ��ڵ�P��D���ҵ�B�ĺ�����Ϊ ![]() ����ô��x�����Ƿ����һ��Q��ʹ��QDPΪ���������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
����ô��x�����Ƿ����һ��Q��ʹ��QDPΪ���������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1���⣺��ͼ1��
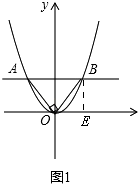
��BE��x�ᣬ
���AOB�ǵ���ֱ�������Σ�
��BE=OE= ![]() AB=1��
AB=1��
��A����1��1����B��1��1����
��A��B����ĺ�����ij˻�Ϊ��1��1=��1��
��������y=ax2��a��0����A��B��
��a=1��
��������y=x2��
��2���⣺��ͼ2��
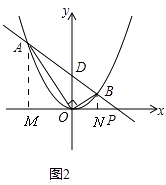
��BN��x�ᣬ��AM��x�ᣬ
���AOB=AMO=��BNO=90�㣬
���MAO=��BON��
���AMO�ס�ONB��
�� ![]() ��
��
��AM��BN=OM��ON��
��A��x1��y1����B��x2��y2�����������ϣ�
��AM=y1=x12��BN=y2=x22��OM=��x1��ON=x2��
��x12��x22=��x1��x2��
��x1��x2=��1��
��A��B���������ij˻���һ����ֵ��
��3���⣺�ɣ�2���ã�A��B���������ij˻���һ����ֵΪ��1��
�ߵ�B�ĺ�����Ϊ ![]() ��
��
���A�ĺ�����Ϊ��2��
��A��B���������ϣ�
��A����2��4����B�� ![]() ��
�� ![]() ����
����
��ֱ��AB����ʽΪy=�� ![]() x+1��
x+1��
��P�� ![]() ��0����D��0��1��
��0����D��0��1��
��Q��n��0����
��DP2= ![]() ��PQ2=��n��
��PQ2=��n�� ![]() ��2��DQ2=n2+1
��2��DQ2=n2+1
�ߡ�QDPΪ���������Σ�
���DP=PQ��
��DP2=PQ2��
�� ![]() =��n��
=��n�� ![]() ��2��
��2��
��n= ![]() ��
��
��Q1�� ![]() ��0����Q2��
��0����Q2�� ![]() ��0��
��0��
��DP=DQ��
��DP2=DQ2��
�� ![]() =n2+1��
=n2+1��
��n= ![]() ���ᣩ��n=��
���ᣩ��n=�� ![]() ��
��
Q3���� ![]() ��0��
��0��
��PQ=DQ��
��PQ2=DQ2��
�ࣨn�� ![]() ��2=n2+1
��2=n2+1
��n=�� ![]() ��
��
��Q4���� ![]() ��0����
��0����
����ڵ�Q����ΪQ1�� ![]() ��0����Q2��
��0����Q2�� ![]() ��0����Q3����
��0����Q3���� ![]() ��0����Q4����
��0����Q4���� ![]() ��0����
��0����
����������1���������������ʼ�����ϵ�������������ʽ��������˻�����2��ͨ������BN��x�ᣬ��AM��x�ᡱ�������������Σ�����AMO�ס�ONB����Ӧ�߳ɱ�����ת��Ϊ�˻�ʽ��A��B���������ij˻���һ����ֵ����3�����ã�2���Ľ������A��B���꣬����QDPΪ���������Σ���������ۣ�����DP=PQ��DP=DQ��PQ=DQ���ֱ����Q����.