Question

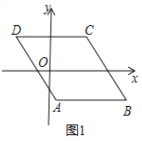
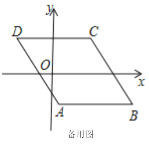
【题目】如图，已知平行四边形ABCD，AC、BD相交于点O，AB=4，AC=6，BD=10．（1）求∠ACD的度数；（2）求BC的长.

Answer 1

【答案】（1）90°；（2） ．

【解析】

（1）由平行四边形ABCD的对角线AC和BD交于点O，若AC=6，BD=10，AB=4，易求得OA与OB的长，又由勾股定理的逆定理，可证得∠BAO=90°，由AB∥CD，可得∠ACD的度数；

（2）在直角△ABC中，利用勾股定理即可求BC的长．

解：（1）∵四边形ABCD是平行四边形，且AC=6，BD=10，AB=4，
∴OA=OC=AC=3，OB=OD=5，
∴OA2+AB2=OB2，
∴△OAB是直角三角形，且∠BAO=90°，

∵AB∥CD，

∴∠ACD=∠BAO=90°；
（2）在直角△ABC中，BC= ．
故答案是：（1）90°；（2） ．