��Ŀ����
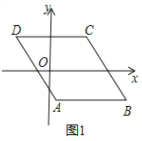
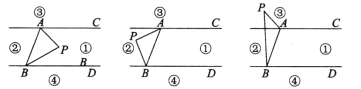
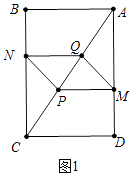
����Ŀ����ͼ���ھ���ABCD�У�AB=3��AD=4����P�ӵ�A������������AC��CB���յ�B�˶�����P��AC�ϵ��ٶ�Ϊÿ��2����λ���ȣ���CB�ϵ��ٶ�Ϊÿ��1����λ���ȣ�ͬʱ����Q�ӵ�A��������AC��ÿ��1����λ���ȵ��ٶ����յ�C�˶�������Q�����յ�ʱ����PҲ��ֹ֮ͣ������P��PM��AD�ڵ�M������QM����PM��QMΪ�ڱ���PMQN����PMQN�����ABCD�ص�����ͼ�ε��ܳ�Ϊd�����ȵ�λ������P���˶�ʱ��Ϊt���룩��t��0��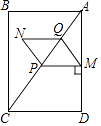
��1����AC�ij�
��2���ú�t�Ĵ���ʽ��ʾ�߶�CP�ij���
��3������P���߶�AC��ʱ����d��t֮��ĺ�����ϵʽ��
��4��������N��ֱ�߽�����ABCD�����ƽ�֣�����ֱ��ͬʱ��PMQN������ֳ�1��3�������֣�ֱ��д����ʱt��ֵ��
���𰸡�
��1���⣺���ı���ABCD�Ǿ��Σ�
��BC=AD=4�����ABC=90�㣬
��Rt��ABC�У���ABC=90�㣬AC= ![]() =
= ![]() =5��
=5��
��AC�ij�Ϊ5��
��2���⣺����P���߶�AC�ϣ�CP=5��2t��
����P���߶�CB�ϣ�CP=t�� ![]() ��
��
��3���⣺��ͼ1�У���N��BC��ʱ��
��AP=2t��AQ=t��
��AQ=PQ��
��PM��AD��
���AMP=90�㣬
��QM= ![]() AP=t��
AP=t��
�ɡ�APM�ס�ACD���ɵ� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��PM= ![]() t��
t��
�ɡ�CNQ�ס�CBA���ɵ� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
���t= ![]() ��
��
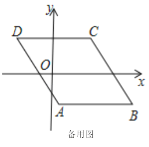
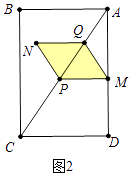
��0��t�� ![]() ʱ����ͼ2�У��ص��������ı���PMQN��
ʱ����ͼ2�У��ص��������ı���PMQN��
d=2��t+ ![]() ��=
��= ![]() t��
t��
�� ![]() ��t��
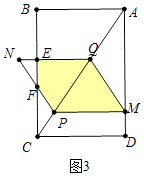
��t�� ![]() ����ͼ3�У��ص������������EFPMQ��
����ͼ3�У��ص������������EFPMQ��
d= ![]() t����1+
t����1+ ![]() ����
���� ![]() ��3��+
��3��+ ![]() ��
�� ![]() t��3��=2t��4��
t��3��=2t��4��
��4���⣺�߾�����N��ֱ�߽�����ABCD�����ƽ�֣�
������ֱ�߾�������ABCD�ĶԽ��ߵĽ���O��
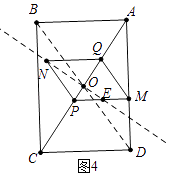
����ͼ4�У���ֱ��ON����PM���е�ʱ��ֱ��ON��PMQN������ֳ�1��3�������֣�
��ʱ����OQ��OP=NQ��PE=2��1���ɵã� ![]() ��t������2t��
��t������2t�� ![]() ��=2��1�����t=
��=2��1�����t= ![]() ��
��
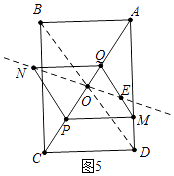
����ͼ5�У���ֱ��ON����QM���е�ʱ��ֱ��ON��PMQN������ֳ�1��3�������֣�
��ʱ����OQ��OP=NQ��PE=1��2���ɵã� ![]() ��t������2t��
��t������2t�� ![]() ��=1��2�����t=
��=1��2�����t= ![]() ��
��
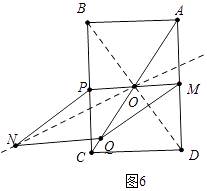
����ͼ6�У�����P��BC�ϣ�PM������Oʱ��ֱ��ON��PMQN������ֳ�1��3�������֣���֪t= ![]() s��
s��
��������������������t��ֵΪt= ![]() s��
s�� ![]() s��
s�� ![]() sʱ��
sʱ��
����������1�����ù��ɶ����ɽ������2����������ۣ�����P���߶�AC�ϣ�CP=5��2t�����P���߶�CB�ϣ�CP=t-![]() ����3���������ķֽ�㣺��N��BC��ʱ���t=
����3���������ķֽ�㣺��N��BC��ʱ���t=![]() ,Ȼ��������ۣ�0��t
,Ȼ��������ۣ�0��t![]()
![]() ,�ص���Ϊ�ı��Σ���
,�ص���Ϊ�ı��Σ���![]() <t<
<t<![]()
![]() ʱ���ص�����Ϊ����Σ��ֱ���t�Ĵ���ʽ��ʾd����4��ƽ�־������������ֱ�߾�������ABCD�ĶԽ��ߵĽ���O���������ۣ��������������ε����ʿ����tֵ��
ʱ���ص�����Ϊ����Σ��ֱ���t�Ĵ���ʽ��ʾd����4��ƽ�־������������ֱ�߾�������ABCD�ĶԽ��ߵĽ���O���������ۣ��������������ε����ʿ����tֵ��
��
�����㾫����������Ҫ�����������ε����ʺ����������ε����ʵ����֪ʶ�㣬��Ҫ�����������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������Σ���Ӧ����ȣ���Ӧ�߳ɱ��������������ν������������β�����ȷ�����⣮