��Ŀ����
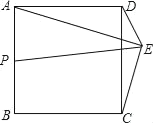
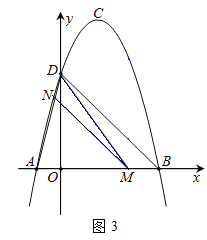
����Ŀ����ͼ��������y��ax2+bx+c��x�ύ�ڵ�A����1��0����B��5��0������y�ύ�ڵ�C��0��![]() ��������ΪD���Գ��ύx���ڵ�E��
��������ΪD���Գ��ύx���ڵ�E��
��1����������ߵ�һ��ʽ��
��2������QΪ���������ϵ�һ������һ���㣬�ҵ�Q�ڶԳ���DE���Ҳ࣬���ı���DEBQ��������ֵ����ʱ��Q�����ꣻ
��3������PΪ�Գ���DE������D��E�Ķ��㣬����D��ֱ��PB�Ĵ��߽�ֱ��PB�ڵ�F����x���ڵ�G������PDGΪ����������ʱ����ֱ��д����P�����꣮
���𰸡���1��y����![]() ����2��
����2��![]() ��Q��
��Q��![]() ��
��![]() ������3����P��������2����
������3����P��������2����![]() ����2��
����2��![]() ��2����2����
��2����2����![]() ��2����2����
��2����2����![]() ��
��
��������
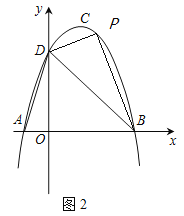
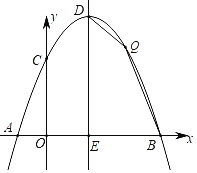
��1����A��B��C���������ֱ�Ӵ������ʽ�������a��b��c��ֵ��
��2������Q��y���ƽ���߽�BD�ڵ�M�����Q��m��![]() �������ֱ��BD�Ľ���ʽΪy��
�������ֱ��BD�Ľ���ʽΪy��![]() ������M��m��
������M��m��![]() ������QM��
������QM��![]() ������S�ı���DEBQ��S��DEB+S��DQM+S��BQM�ɵó�m�ı���ʽ���ɶ��κ��������ʿ�����𰸣�
������S�ı���DEBQ��S��DEB+S��DQM+S��BQM�ɵó�m�ı���ʽ���ɶ��κ��������ʿ�����𰸣�
��3�����P��2��n�����ɵó���G��2��![]() ��0�����ֵ�GP��GD��GP��PD��GD��PD����������ó�n�ķ��̷ֱ���⼴�ɣ�
��0�����ֵ�GP��GD��GP��PD��GD��PD����������ó�n�ķ��̷ֱ���⼴�ɣ�
�⣺��1����A����1��0����B��5��0����C��0��![]() �������������߽���ʽ�ã�
�������������߽���ʽ�ã�
 ����ã�
����ã� ��
��
�������߽���ʽΪ��y����![]() ��
��
��2���������߽���ʽΪy����![]() ����
����![]() ��
��
�������ߵĶ���D������Ϊ��2��![]() �����Գ���Ϊx��2��E��2��0����
�����Գ���Ϊx��2��E��2��0����
����Q��y���ƽ���߽�BD�ڵ�M�����Q��m��![]() ����
����

��ֱ��BD�Ľ���ʽΪy��kx+b��
��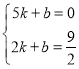 ��
��
��ã�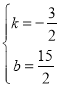 ��
��
��ֱ��BD�Ľ���ʽΪy��![]() ��
��
����M��m��![]() ����
����
��QM��![]() ����
����![]() ����
����![]() ��
��
��S�ı���DEBQ��S��DEB+S��DQM+S��BQM
��![]() +
+![]() ����m��2��+
����m��2��+![]() ��
��
��![]() ��
��
��m��![]() ʱ��S�ı���DEBQȡ�����ֵ��S�ı���DEBQ��
ʱ��S�ı���DEBQȡ�����ֵ��S�ı���DEBQ��![]() ��
��
��ʱ![]() ��
��
��Q��![]() ��
��![]() ����
����
��3�������ߵĶԳ���Ϊx��2�����D��2��![]() ����
����
���P��2��n����
����P��B���������һ�κ�������ʽ��y��sx+t����ã�
����PB�ı���ʽΪ��y��![]() ��
��
��DG��PB��
��ֱ��DG����ʽ�е�kֵΪ![]() ��
��
����D���������һ�κ�������ʽ��
ͬ���ɵ�ֱ��DG�ı���ʽΪ��y��![]() ��
��
��ã�x��2��![]() ��
��
�ʵ�G��2��![]() ��0����
��0����
��GP2��![]() ��
��![]() ��
��![]() ��
��
�ٵ�GP��GDʱ��![]()
![]() ��
��
��ã�n����![]() ��
��![]() ����ȥ����
����ȥ����
��P��2����![]() ����
����
�ڵ�GP��PDʱ��![]() ��
��
��ã�n����2��![]() ��
��
��P��2����2+![]() ����P��2����2��
����P��2����2��![]() ����
����
�۵�GD��PDʱ��![]() ��
��
��ã�n����![]() ��n��0����ȥ����
��n��0����ȥ����
��P��2��![]() ����
����
�ۺ���������P������Ϊ��2����![]() ����2��
����2��![]() ��2����2����
��2����2����![]() ��2����2����
��2����2����![]() ����
����

����Ŀ��ijУΪ�˽��ߡ����꼶ѧ����������ˮ����ȫ֪ʶ��������������ߡ����꼶�������ȡ50��ѧ�����в��ԣ����Գɼ����ٷ��ƣ����������������ͷ�����������Ϣ���£�
a�����꼶�ɼ�Ƶ���ֲ�ֱ��ͼ��

b�����꼶�ɼ���![]() ��һ����ǣ�70 72 74 75 76 76 77 77 77 78 79
��һ����ǣ�70 72 74 75 76 76 77 77 77 78 79
c���ߡ����꼶�ɼ���ƽ��������λ�����£�
�꼶 | ƽ���� | ��λ�� |
�� | 76.9 | m |
�� | 79.2 | 79.5 |
����������Ϣ���ش��������⣺
��1������β����У����꼶��80�����ϣ���80�֣������� ���ˣ�
��2������m��ֵΪ�� ����
��3������β����У����꼶ѧ��������꼶ѧ���ҵijɼ�����78�֣����ж���λѧ���ڸ����꼶������˭����ǰ����˵�����ɣ�
��4����У���꼶ѧ����400�ˣ�����ȫ���μӴ˴β��ԣ���������꼶�ɼ�����ƽ����76.9�ֵ�������