题目内容
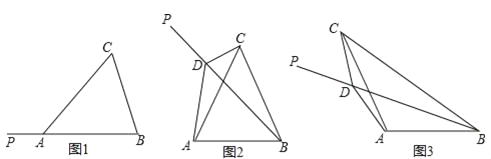
【题目】如图,正方形ABCD的边长为2![]() ,点E为正方形外一个动点,∠AED=45°,P为AB中点,线段PE的最大值是_____.
,点E为正方形外一个动点,∠AED=45°,P为AB中点,线段PE的最大值是_____.
【答案】![]()
【解析】
当点E在正方形右侧时,连接AC,BD交于点O,连接PO,EO,根据A,C,E,D四点共圆,可得OE=OD=![]() ,再根据PE≤OP+OE=
,再根据PE≤OP+OE=![]() ,可得当点O在线段PE上时,PE=OP+OE=
,可得当点O在线段PE上时,PE=OP+OE=![]() ,则线段PE的最大值为
,则线段PE的最大值为![]() ;
;
当点E在正方形上方时,作斜边为AD的等腰直角△AOD,则点E在以O为圆心,OA为半径的圆上,当点P,点O,点E共线时,PE的值最大,求得此时PE最大值为![]() ;比较两个最大值,可得最终结果.
;比较两个最大值,可得最终结果.
解:如图,若点E在正方形右侧,连接AC,BD交于点O,连接PO,EO,
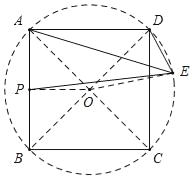
∵∠AED=45°,∠ACD=45°,
∴A,C,E,D四点共圆,
∵正方形ABCD的边长为2![]() ,
,
∴OE=OD=![]() BD=
BD=![]() ,
,
∵P为AB的中点,O是BD的中点,
∴OP=![]() AD=
AD=![]() ,
,
∵PE≤OP+OE=![]() +
+![]() ,
,
∴当点O在线段PE上时,PE=OP+OE=![]() +
+![]() ,
,
即线段PE的最大值为![]() +
+![]() ,
,
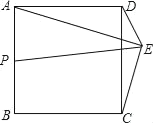
如图,点E在正方形ABCD上方,
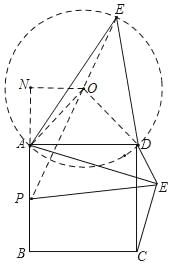
作斜边为AD的等腰直角△AOD,∠AOD=90°,
则点E在以O为圆心,OA为半径的圆上,
∴当点P,点O,点E共线时,PE的值最大,
过点O作ON⊥AB,交BA延长线于点N,
∵AD=2![]() ,AO=DO,∠AOD=90°
,AO=DO,∠AOD=90°
∴AO=![]() ,∠OAD=45°,
,∠OAD=45°,
∵ON⊥AB,AD⊥AB
∴∠NAO=∠NOA=45°
∴AN=NO=![]()
∴PO=![]()
∴PE最大值为![]() ,
,
故答案为![]() .
.

 尖子生新课堂课时作业系列答案
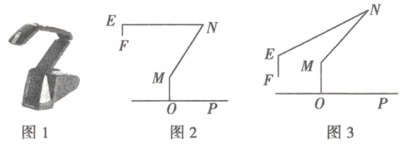
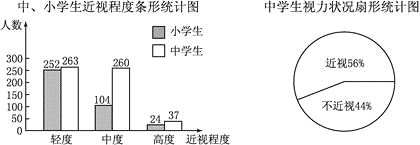
尖子生新课堂课时作业系列答案【题目】某商店在开业前,所进三种货物:上衣、裤子和鞋子的数量共480份,这三种货物进货的数量比例如图(1)所示.商店安排6人只销售上衣,4人只销售裤子,2人只销售鞋子,用了5天的时间销售货物的情况如图(2)及表格所示.
(1)求所进三种货物中上衣有多少件?
(2)直接在图中把图(2)补充完整;
(3)表格中的![]() = (直接填空);
= (直接填空);
(4)若销售人员不变,并以同样的销售速度销售,则上衣、裤子和鞋子中最先销售完的货物为 (直接填空).

货物 | 上衣(件) | 裤子(条) | 鞋子(双) |
5天的销售总额 | 150 | a | 30 |
【题目】某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克至60千克之间(含20千克和60千克)时,每千克批发5元;若超过60千克是,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)根据题意,填写如表:
蔬菜的批发量(千克) | ... | 25 | 60 | 75 | 90 | ... |
所付的金额(元) | ... | 125 | 300 | ... |
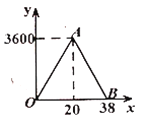
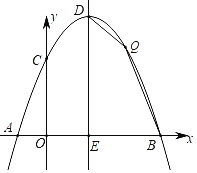
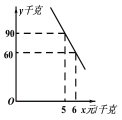
(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量![]() (千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出
(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润是多少?