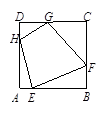题目内容
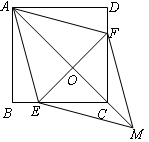
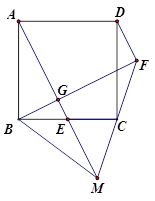
已知：如图所示的一张矩形纸片ABCD(AD＞AB)，将纸片折叠一次，使点A与点C重合，再展开，折痕EF交AD边于点E，交BC边于点F，分别连结AF和CE．
(1)求证：四边形AFCE是菱形；
(2)若AE=5cm，△CDE的周长为12cm，求矩形ABCD的面积．
(1)求证：四边形AFCE是菱形；
(2)若AE=5cm，△CDE的周长为12cm，求矩形ABCD的面积．
有一组邻边相等的平行四边形是菱形；(2)S矩形ABCD=27cm2或32cm2；
试题分析：证明：由于点A与点C重合，所以EF垂直平分AC，所以AFCE是平行四边形
又因为OE="OF,"
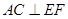，所以四边形AFCE是菱形；由题意知AE=EC=5，设DE=X则有CD=7-X,,因为AD=5+X，
AD大于AB,所以
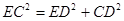
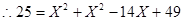
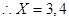
所以S矩形ABCD=27cm2或32cm2
点评：本题属于对菱形的基本判定定理的运用和菱形性质的解题
练习册系列答案
阅读快车系列答案
相关题目
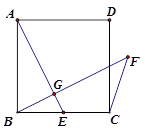
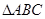中，D是AB中点，E是AC上的点，且
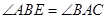，EF∥AB，DF∥BE，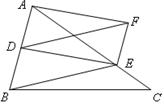 
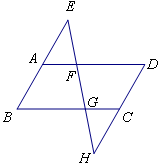
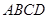中，
,
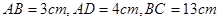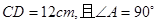，则四边形
