题目内容
在边长为2的正方形ABCD的四边上分别取点E、F、G、H、四边形EFGH四边的平方和EF2+FG2+GH2+HE2最小时其面积为 .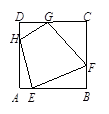
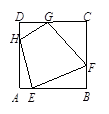
2
试题分析:利用勾股定理列出四边形EFGH四边的关系,利用配方法求得E、F、G、H为正方形ABCD四边的中点,从而问题得解.
在正方形ABCD中,
∠A=∠B=∠C=∠D=90°,
AB=BC=CD=DA=2;
∴EF2+FG2+GH2+HE2=BE2+BF2+CF2+CG2+GD2+DH2+AH2+AE2,
=BE2+BF2+(2-BF)2+CG2+(2-CG)2+DH2+(2-DH)2+(2-BE)2,
=2(BE-1)2+2(BF-1)2+2(CG-1)2+2(DH-1)2+8≥8,
当EF2+FG2+GH2+HE2最小为8时,可得,
AE=BE=BF=CF=CG=DG=DH=AH,
即E、F、G、H为正方形ABCD四边的中点,
由此得出四边形EFGH为正方形,其面积为EF2=BF2+BE2=2.
点评:解题的关键是熟练掌握正方形的四条边相等,四个角都是直角.

练习册系列答案
相关题目

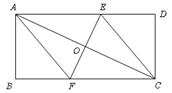
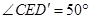 ,则
,则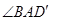 的大小是
的大小是 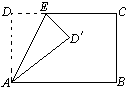
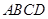 的周长为52cm,对角线
的周长为52cm,对角线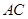 、
、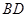 交于点
交于点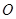 ,且
,且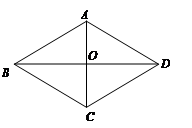
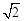 ≈1.4,
≈1.4,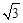 ≈1.7).
≈1.7).