Question

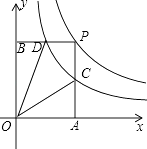
【题目】如图，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y= 在第一象限的图象经过点B，则△OAC与△BAD的面积之差S△OAC﹣S△BAD为（ ）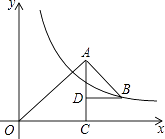
A.36
B.12
C.6
D.3

Answer 1

【答案】D
【解析】解：设△OAC和△BAD的直角边长分别为a、b， 则点B的坐标为（a+b，a﹣b）．
∵点B在反比例函数y= 的第一象限图象上，
∴（a+b）×（a﹣b）=a2﹣b2=6．
∴S△OAC﹣S△BAD= a2﹣ b2= （a2﹣b2）= ×6=3．
故选D．
设△OAC和△BAD的直角边长分别为a、b，结合等腰直角三角形的性质及图象可得出点B的坐标，根据三角形的面积公式结合反比例函数系数k的几何意义以及点B的坐标即可得出结论．