Question

【题目】如图，菱形ABCD中，对角线AC、BD相交于点O，点E是AB的中点，已知AC=8cm，BD=6cm，求OE的长．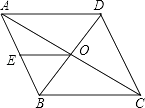

Answer 1

【答案】解：∵ABCD是菱形 ∴OA=OC，OB=OD，OB⊥OC
又∵AC=8cm，BD=6cm
∴OA=OC=4cm，OB=OD=3cm
在直角△BOC中，
由勾股定理，得BC= =5cm
∵点E是AB的中点
∴OE是△ABC的中位线，
∴OE= cm．
【解析】根据菱形的性质及中位线定理解答．
【考点精析】本题主要考查了勾股定理的概念和三角形中位线定理的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半才能正确解答此题．