Question

【题目】如图是函数y= 与函数y= 在第一象限内的图象，点P是y= 的图象上一动点，PA⊥x轴于点A，交y= 的图象于点C，PB⊥y轴于点B，交y= 的图象于点D．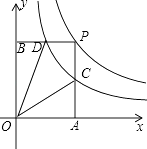
（1）求证：D是BP的中点；
（2）求四边形ODPC的面积．

Answer 1

【答案】
（1）证明：∵点P在函数y= 上，

∴设P点坐标为（ ，m）．

∵点D在函数y= 上，BP∥x轴，

∴设点D坐标为（ ，m），

由题意，得

BD= ，BP= =2BD，

∴D是BP的中点

（2）解：S四边形OAPB= m=6，

设C点坐标为（x， ），D点坐标为（ ，y），

S△OBD= y = ，

S△OAC= x = ，

S四边形OCPD=S四边形PBOA﹣S△OBD﹣S△OAC=6﹣ ﹣ =3

【解析】（1）根据函数图象上的点满足函数解析式，可得P、D点坐标，根据线段中点的定义，可得答案；（2）根据图象割补法，可得面积的和差，可得答案．