题目内容
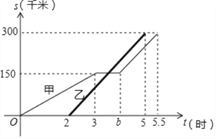
【题目】甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,设甲、乙两车与A地的路程为s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
(1)求a和b的值.
(2)求两车在途中相遇时t的值.
(3)当两车相距60千米时,t= 时.
【答案】(1)50,4;(2)t的值为3.5.(3)![]() 或
或![]() .
.
【解析】试题分析:(1)根据速度=路程÷时间即可求出a值,再根据时间=路程÷速度算出b到5.5之间的时间段,由此即可求出b值; (2)观察图形找出两点的坐标,利用待定系数法即可求出s乙关于t的函数关系式,令s乙=150即可求出两车相遇的时间;(3)分0≤t≤3 、3≤t≤4 和4≤t≤5.5三段求出关于t的函数关系式,二者做差令其绝对值等于60即可得出关于t的函数绝对值符号的一元一次方程,解之即可求出t值,再求出0≤t≤2时,s甲=50t=60中t的值,综上即可得出结论.
试题解析:
(1)a=![]() =50,b=5.5-
=50,b=5.5-![]() =4.
=4.
(2)设乙车与A地的路程s与甲车离开A地的时间t之间的函数关系式为s乙=kt+m,
将(2,0)、(5,300)代入s=kt+m,
![]() ,
,
解得: ![]() ,
,
∴s乙=100t-200(2≤t≤5).
当s乙=100t-200=150时,t=3.5.
答:两车在途中相遇时t的值为3.5.
(3)当0≤t≤3时,s甲=50t;
当3≤t≤4时,s甲=150;
当4≤t≤5.5时,s甲=150+2×50(t-4)=100t-250.
∴s甲= .
.
令|s甲-s乙|=60,即|50t-100t+200|=60,|150-100t+200|=60或|100t-250-100t+200|=60,
解得:t1=![]() ,t2=
,t2=![]() (舍去),t3=
(舍去),t3=![]() (舍去),t4=
(舍去),t4=![]() (舍去);
(舍去);
当0≤t≤2时,令s甲=50t=60,解得:t=![]() .
.
综上所述:当两车相距60千米时,t=![]() 或
或![]() .
.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案