题目内容
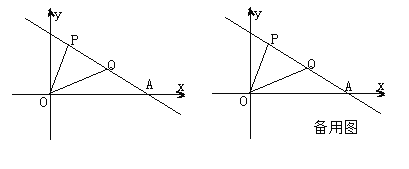
【题目】已知一次函数y=kx+b的图象过P(1,4),Q(4,2)两点,且与x轴交于A点.
(1)求A点坐标;
(2)已知点M在x轴上,若使MP+MQ的值最小,求点M的坐标及MP+MQ的最小值;
(3)在(2)的条件下,在坐标平面内是否还存在一点N,使M,N,A,Q四点恰好构成平行四边形,若存在请求出点N的坐标,若不存在请说明理由。
【答案】(1) A(7,0);(2)3![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)把P(1,4),Q(4,2)代入y=kx+b,利用待定系数法即可求出此一次函数的解析式,然后得出点A的坐标;(2) 作Q点关于x轴的对称点Q′,连接PQ′交x轴于点M,根据两点之间线段最短得出此时MP+MQ的值最小.利用待定系数法求出直线PQ′的解析式,进而求出点M的坐标及MP+MQ即可.
解:(1)∵一次函数y=kx+b的图象过P(1,4),Q(4,2)两点,
∴函数解析式为:![]()
∴直线PQ和x轴交于A(7,0);
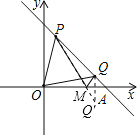
(2)作Q点关于x轴的对称点Q′(4,-2),连接PQ′交x轴于点M,则MP+MQ的值最小,
∵P(1,4), Q′(4,-2), ∴P Q′=![]() ,此时MP+MQ最小,∴(MP+MQ)最小=P Q′=
,此时MP+MQ最小,∴(MP+MQ)最小=P Q′=![]()
(3)存在N(6,-2),(8,2)或N(0,2),
理由:如图:

①∵A(7,0),M(3,0),
∴在平行四边形MA![]() Q中,Q
Q中,Q![]() =AM=7-3=4, ∵Q
=AM=7-3=4, ∵Q![]() ∥x轴,∴
∥x轴,∴![]() (8,2);
(8,2);
②在平行四边形MAQ![]() 中,Q
中,Q![]() =AM=7-3=4,而Q
=AM=7-3=4,而Q![]() ∥x轴,∴
∥x轴,∴![]() (0,2);
(0,2);
③在平行四边形QM![]() A中, ∵MQ=A
A中, ∵MQ=A![]() ,∠QME=
,∠QME=![]() AF, ∠QEM=∠
AF, ∠QEM=∠![]() FA=90°,
FA=90°,
∴△QME≌△![]() AF, ∴QE=F
AF, ∴QE=F![]() =2,AF=ME=4-3=1, ∴OF=6, ∴
=2,AF=ME=4-3=1, ∴OF=6, ∴![]() (6,-2),
(6,-2),
综上所述:N(6,-2),(8,2)或N(0,2).

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案【题目】温度通常有两种表示方法:华氏度(单位:![]() )与摄氏度(单位:
)与摄氏度(单位:![]() ).已知华氏度数y与摄氏度数x之间是一次函数关系.下表列出了部分华氏度与摄氏度之间的对应关系.
).已知华氏度数y与摄氏度数x之间是一次函数关系.下表列出了部分华氏度与摄氏度之间的对应关系.
摄氏度数x( | … | 0 | … | 35 | … | 100 | … |
华氏度数y( | … | 32 | … | 95 | … | 212 | … |
(1)选用表格中给出的数据,求y关于x的函数解析式(不需要写出该函数的定义域);
(2)已知某天的最低气温是![]()
![]() ,求与之对应的华氏度数.
,求与之对应的华氏度数.