题目内容
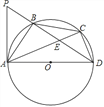
【题目】如图,△ABC内接于⊙O,且AB=BC.AD是⊙O的直径,AC、BD交于点E,P为DB延长线上一点,且PB=BE.
(1)求证:△ABE∽△DBA;
(2)试判断PA与⊙O的位置关系,并说明理由;
(3)若E为BD的中点,求tan∠ADC的值.
【答案】(1)证明见解析;(2)PA与⊙O相切,理由见解析;(3)2![]() .
.
【解析】分析: (1)先判断出弧AB=弧BC,进而得出∠ADB=∠BAE,即可得出结论;
(2)先判断出AB是PE的垂直平分线,进而得出∠BAP=∠BAE,即可得出结论;
(3)先利用相似得出AB,进而用勾股定理的粗话AE,再判断出△ABE∽△DCE,进而求出CD,CE,即可得出AC,即可得出结论.
详解:
(1)证明:∵AB=BC,
∴![]() ,
,
∴∠ADB=∠BAE,
∵∠ABE=∠DBA,
∴△ABE∽△DBA;
(2)解:PA与⊙O相切,
理由:∵AD是⊙O的直径,
∴∠ABD=90°,
∵PB=BE,
∴AB是PE的垂直平分线,
∴AP=AE,
∴∠BAP=∠BAE,
∵∠ADB=∠BAE,
∴∠BAP=∠ADB,
∵∠DAB+∠BDA=90°,
∴∠DAB+BAP=90°,
∵点A在⊙O上,
∴PA与⊙O相切;
(3)解:设BE=DE=a,则BD=2a,
∵△ABE∽△DBA,
∴![]() ,
,
∴![]() ,
,
∴AB=![]() a,
a,
根据勾股定理得,AE=![]() =
=![]() a,
a,
∵![]() ,
,
∴∠BAE=∠CDE,
∵∠AEB=∠DEC,
∴△ABE∽△DCE,
∴![]() ,
,
∴![]() ,
,
∴CD=![]() a,CE=
a,CE=![]() a,
a,
∴AC=AE+CE=![]() ,
,
∵AD是⊙O直径,
∴∠ACD=90°,
在Rt△ACD中,tan∠ADC=![]() =2
=2![]() .
.
点睛: 此题是圆的综合题,主要考查了圆的性质,切线的判定和性质,线段的垂直平分线,相似三角形的判定和性质,锐角三角函数,判断出△ABE∽△DCE是解本题的关键.

【题目】2019年7月9日,北京市滴滴快车调整了价格,规定车费由“总里程费+总时长费”两部分构成,具体收费标准如下表:(注:如果车费不足起步价,则按起步价收费.)
时间段 | 里程费(元/千米) | 时长费(元/分钟) | 起步价(元) |
06:00—10:00 | 1.80 | 0.80 | 14.00 |
10:00—17:00 | 1.45 | 0.40 | 13.00 |
17:00—21:00 | 1.50 | 0.80 | 14.00 |
21:00—06:00 | 2.15 | 0.80 | 14.00 |
(1)小明07:10乘快车上学,行驶里程6千米,时长10分钟,应付车费 元;
(2)小芳17:20乘快车回家,行驶里程1千米,时长15分钟,应付车费 元;
(3)小华晚自习后乘快车回家,20:45在学校上车.由于道路施工,车辆行驶缓慢,15分钟后选择另外道路,改道后速度是改道前速度的3倍,10分钟后到家,共付了车费37.4元,问从学校到小华家快车行驶了多少千米?
【题目】已知一水池的容积V(公升)与注入水的时间t(分钟)之间开始是一次函数关系,表中记录的是这段时间注入水的时间与水池容积部分对应值.
注入水的时间t(分钟) | 0 | 10 | … | 25 |
水池的容积V(公升) | 100 | 300 | … | 600 |
(1)求这段时间时V关于t的函数关系式(不需要写出函数的定义域);
(2)从t为25分钟开始,每分钟注入的水量发生变化了,到t为27分钟时,水池的容积为726公升,如果这两分钟中的每分钟注入的水量增长的百分率相同,求这个百分率.