��Ŀ����
����Ŀ����ϣ���ϴ����˹ѧ�ɵ���ѧ�Ҿ�����Сʯ�Ӱڳɸ�����״���о���ѧ���⣮
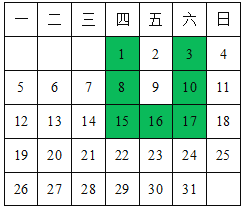
��ͼ1��������Щ����������1����3����6����10������ Сʯ�Ӱڳɵģ��������dz�1��3��6��10��������Щ��Ϊ�������������Ƶģ���ͼ2�����dz�1��4��9��16��������������Ϊ�ı�������

��1���������������������ı��������Ҵ���1����С�������� ��
��2������ǵ�n��k����Сʯ�ӵĸ���Ϊ![]() ��k��3������ô��
��k��3������ô��![]() ��
��![]() ��
��![]() ��
��
�� ![]() ��
��![]() ��
��
�� ![]() ��
��![]() ��
��
�� ���![]() ����ô
����ô![]() ��
��
��3�������һ���о�����![]() ��
��![]() ��������ô
��������ô![]() ��
��
���𰸡���1��36����2���� 6��81����![]() ��
��![]() ���� 10����3��1 000��
���� 10����3��1 000��
��������
��1��ͼ1��1��3��6��10��������n��ͼ�е�ĸ�����1+2+3+��+n����![]() ��ͼ2��1��4��9��16��������n��ͼ�е�ĸ�����n2�������ͬʱ��������ʽ�ӵ��������ɵó������
��ͼ2��1��4��9��16��������n��ͼ�е�ĸ�����n2�������ͬʱ��������ʽ�ӵ��������ɵó������
��2����ͼ1��1��3��6��10��������n��ͼ�е�ĸ�����1+2+3+��+n����![]() ��ͼ2��1��4��9��16��������n��ͼ�е�ĸ�����n2�����ɵó������
��ͼ2��1��4��9��16��������n��ͼ�е�ĸ�����n2�����ɵó������
��3����M��n��3��![]() ��M��n��4��
��M��n��4��![]() ��M��n��5��
��M��n��5��![]() ��M��n��6��
��M��n��6��![]() �����ƶ�M��n��k��
�����ƶ�M��n��k��![]() ��k��3������M��10��24�����뼴�ɵó������
��k��3������M��10��24�����뼴�ɵó������
��1�����ı�������ĸ�����Ϊn2��
���1�⣬�ֱ�Ϊ4��9��16��25��36��49��64������
��ͼ1��1��3��6��10��������n��ͼ�е�ĸ�����1+2+3+��+n��������������ĸ�����Ϊ![]() ��
��
��4![]() ���������⣬
���������⣬
��4��������������
��9![]() ���������⣬
���������⣬
��9��������������
��16![]() ���������⣬
���������⣬
��16��������������
��25![]() ���������⣬
���������⣬
��25��������������
��36![]() ����ã�n=8������36������������
����ã�n=8������36������������
���1�⣬��С�ļ����������������ı���������36��
�ʴ�Ϊ��36��
��2���ɣ�1��֪��M��n��3��![]() ��M��n��4��=n2��
��M��n��4��=n2��
�ʣ���M��3��3��=![]() =6��M��9��4��=92=81��
=6��M��9��4��=92=81��
��M��n��3��![]() ��M��n��4��=n2��
��M��n��4��=n2��
��M��n��3��![]() =55��
=55��
��n2+n-110=0��
�ࣨn-10����n+11��=0��
��ã�n=10��n=-11����ȥ����
��n=10��
��3����M��n��3��![]() ��
��
M��n��4��=n2![]() ��
��
M��n��5��![]() n2
n2![]() n
n![]() ��
��
M��n��6��=2n2��n![]() ��
��
���ɴ˱仯���ɿ��ƶ�M��n��k��![]() ��k��3����
��k��3����
��M��10��24��![]() 1000��
1000��

����Ŀ��2019��7��9�գ������еεο쳵�����˼۸涨�����ɡ�����̷�+��ʱ���ѡ������ֹ��ɣ������շѱ����±�����ע��������Ѳ����ۣ������շѣ���
ʱ��� | ��̷ѣ�Ԫ/ǧ�ף� | ʱ���ѣ�Ԫ/���ӣ� | �ۣ�Ԫ�� |
06:00��10:00 | 1.80 | 0.80 | 14.00 |
10:00��17:00 | 1.45 | 0.40 | 13.00 |
17:00��21:00 | 1.50 | 0.80 | 14.00 |
21:00��06:00 | 2.15 | 0.80 | 14.00 |
��1��С��07:10�˿쳵��ѧ����ʻ���6ǧ�ף�ʱ��10���ӣ�Ӧ������ Ԫ��
��2��С��17:20�˿쳵�ؼң���ʻ���1ǧ�ף�ʱ��15���ӣ�Ӧ������ Ԫ��
��3��С������ϰ��˿쳵�ؼң�20:45��ѧУ�ϳ������ڵ�·ʩ����������ʻ������15���Ӻ�ѡ�������·���ĵ����ٶ��Ǹĵ�ǰ�ٶȵ�3����10���Ӻң������˳���37.4Ԫ���ʴ�ѧУ��С���ҿ쳵��ʻ�˶���ǧ�ף�