题目内容
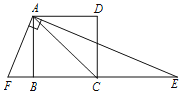
【题目】如图，正方形ABCD边长为3，连接AC，AE平分∠CAD，交BC的延长线于点E，FA⊥AE，交CB延长线于点F，则EF的长为__________．
【答案】6
【解析】试题分析：利用正方形的性质和勾股定理可得AC的长，由角平分线的性质和平行线的性质可得∠CAE=∠E，易得CE=CA，由FA⊥AE，可得∠FAC=∠F，易得CF=AC，可得EF的长．
∵四边形ABCD为正方形，且边长为3， ∴AC=3， ∵AE平分∠CAD， ∴∠CAE=∠DAE，
∵AD∥CE， ∴∠DAE=∠E， ∴∠CAE=∠E， ∴CE=CA=3， ∵FA⊥AE，
∴∠FAC+∠CAE=90°，∠F+∠E=90°， ∴∠FAC=∠F， ∴CF=AC=3，
∴EF=CF+CE=3+3=6
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
【题目】根据国家发改委实施“阶梯水价”文件要求，某市结合地方实际，决定从2016年1月1日起对居民生活用水按新的“阶梯水价”标准收费，某中学研究学习小组的同学们在社会实践活动中调查了30户家庭某月的用水量，如表所示：
用水量（吨） | 15 | 20 | 25 | 30 | 35 |
户数 | 3 | 6 | 7 | 9 | 5 |
则这30户家庭该月用水量的众数和中位数分别是（ ）
A. 25，27 B. 30，25 C. 30，27 D. 25，25
