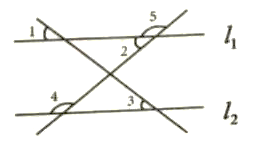
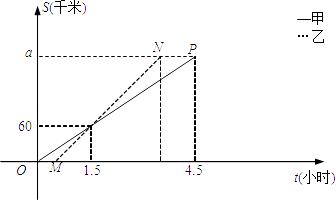
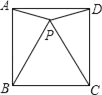
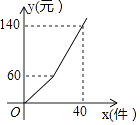题目内容
【题目】用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案:

![]()
![]()
![]()
⑴ 当黑砖n=1时,白砖有_______块,当黑砖n=2时,白砖有________块,
当黑砖n=3时,白砖有_______块.
⑵ 第n个图案中,白色地砖共 块.
【答案】(1)6 10 14 (2)4n+2
【解析】【试题分析】(1)当n=1时,白砖有6块;当n=2时,白砖有10块,当n=3时,白砖有14块;(2)n每增加1,白色地砖增加4块,则第n个图案中,白色地砖共(4n+2)块
【试题解析】
当n=1时,白砖有6块;当n=2时,白砖有10块,当n=3时,白砖有14块;
(2)n每增加1,白色地砖增加4块,则第n个图案中,白色地砖共4(n-1))+6=4n+2(块)

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
【题目】小张买了张![]() 元的乘车IC卡,如果他乘车的次数用
元的乘车IC卡,如果他乘车的次数用![]() 表示,则记录他每次乘车后的余额
表示,则记录他每次乘车后的余额![]() (元)如下表:
(元)如下表:
次数m | 余额n(元) |
1 | 50—0.8 |
2 | 50—1.6 |
3 | 50—2.4 |
4 | 50—3.2 |
…… | …… |
【1】⑴写出乘车的次数![]() 表示余额
表示余额![]() (元)的关系式;
(元)的关系式;
【2】⑵利用上述关系式计算小张乘了13次车后还剩下多少元?
【3】⑶小张最多能乘几次车?