题目内容
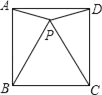
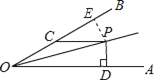
【题目】如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为_____.

【答案】2
【解析】
过P作PE垂直与OB,由∠AOP=∠BOP,PD垂直于OA,利用角平分线定理得到PE=PD,由PC与OA平行,根据两直线平行得到一对内错角相等,又OP为角平分线得到一对角相等,等量代换可得∠COP=∠CPO,又∠ECP为三角形COP的外角,利用三角形外角的性质求出∠ECP=30°,在直角三角形ECP中,由30°角所对的直角边等于斜边的一半,由斜边PC的长求出PE的长,即为PD的长.
过P作PE⊥OB,交OB与点E,
∵∠AOP=∠BOP,PD⊥OA,PE⊥OB,
∴PD=PE,
∵PC∥OA,
∴∠CPO=∠POD,
又∠AOP=∠BOP=15°,
∴∠CPO=∠BOP=15°,
又∠ECP为△OCP的外角,
∴∠ECP=∠COP+∠CPO=30°,
在直角三角形CEP中,∠ECP=30°,PC=4,
∴PE=![]() PC=2,
PC=2,
则PD=PE=2.
故答案为:2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目