��Ŀ����
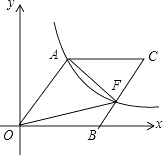
����Ŀ����ͼ����֪��BAD�͡�BCE��Ϊ����ֱ�������Σ���BAD=��BCE=90�㣬��MΪDE���е㣬����E��ADƽ�е�ֱ�߽�����AM�ڵ�N��
��1����A��B��C������ͬһֱ����ʱ����ͼ1����ֱ��д���߶�AD��NE��������ϵΪ �� 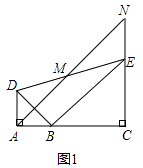
��2����ͼ1�еġ�BCE�Ƶ�B��ת����A��B��E������ͬһֱ����ʱ����ͼ2�����жϡ�ACN��ʲô���������β�˵�����ɣ�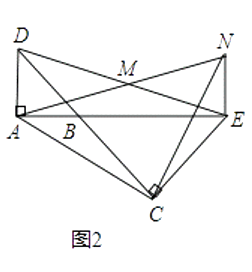
��3����ͼ1�С�BCE�Ƶ�B��ת��ͼ3λ�ã���ʱA��B��M������ͬһֱ���ϣ���AC=3 ![]() ��AD=1�����ı���ACEN�����Ϊ ��
��AD=1�����ı���ACEN�����Ϊ �� 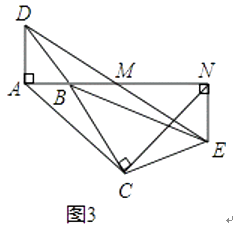
���𰸡�
��1��AD=NE
��2���⣺��2�����ۣ���ACNΪ����ֱ�������Σ�
���ɣ���ͼ2��
�ߡ�BAD�͡�BCE��Ϊ����ֱ�������Σ�
��AB=AD��CB=CE����CBE=��CEB=45�㣮
��AD��NE��
���DAE+��NEA=180�㣮
�ߡ�DAE=90�㣬
���NEA=90�㣮
���NEC=135�㣮
��A��B��E������ͬһֱ���ϣ�
���ABC=180�㩁��CBE=135�㣮
���ABC=��NEC��
�ߡ�ADM�ա�NEM����֤����
��AD=NE��
��AD=AB��
��AB=NE��
�ڡ�ABC�͡�NEC�У�
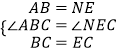 ��
��
���ABC�ա�NEC��
��AC=NC����ACB=��NCE��
���ACN=��BCE=90�㣮
���ACNΪ����ֱ��������
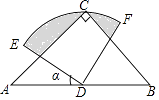
��3��![]()
���������⣺��1�����ۣ�AD=NE��
���ɣ���ͼ1��
��EN��AD��
���MAD=��MNE����ADM=��NEM��
�ߵ�MΪDE���е㣬
��DM=EM��
�ڡ�ADM�͡�NEM�У�
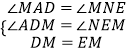 ��
��
���ADM�ա�NEM��
��AD=NE��
�⣺��3����ͼ3�У�����CM��

��AD��NE��MΪ�е㣬
���á�ADM�ա�NEM��
��AD=NE��
��AD=AB��
��AB=NE��
��AD��NE��
��AF��NE��
���ı���BCEF�У�
�ߡ�BCE=��BFE=90��
���FBC+��FEC=360�㩁180��=180��
�ߡ�FBC+��ABC=180��
���ABC=��FEC
�ڡ�ABC�͡�NEC�У�
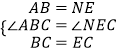 ��
��
���ABC�ա�NEC��
��AC=NC����ACB=��NCE��
���ACN=��BCE=90�㣮
���ACNΪ����ֱ�������Σ�
�ɣ�1����֪����AMD�ա�NME��
��AM=MN��AD=NE=1��
��CM��AN��AM=CM=MN��
��AC=3 ![]() ��
��
��AM=CM=MN=3��
��S�ı���ACNE=S��AMC+Sֱ������MNEC= ![]() ��3��3+
��3��3+ ![]() ����3+1����3=
����3+1����3= ![]() ��
��
���Դ��� ![]() ��
��
�����㾫����ͨ�����������ת�����ʣ����բ���ת���Ӧ���߶γ��̲��䣬��ת�Ƕȴ�С���䣻����ת���Ӧ�ĵ㵽��ת����ת���ĵľ��벻�䣻����ת�������ͼ�β��䣬ֻ��λ�ñ��˼����Խ����⣮

 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�����Ŀ��С��������![]() Ԫ�ij˳�IC����������˳��Ĵ�����
Ԫ�ij˳�IC����������˳��Ĵ�����![]() ��ʾ�����¼��ÿ�γ˳�������
��ʾ�����¼��ÿ�γ˳�������![]() ��Ԫ�����±���
��Ԫ�����±���
����m | ���n��Ԫ�� |
1 | 50��0.8 |
2 | 50��1.6 |
3 | 50��2.4 |
4 | 50��3.2 |
���� | ���� |
��1����д���˳��Ĵ���![]() ��ʾ���
��ʾ���![]() ��Ԫ���Ĺ�ϵʽ��
��Ԫ���Ĺ�ϵʽ��
��2��������������ϵʽ����С�ų���13�γ���ʣ�¶���Ԫ��
��3����С������ܳ˼��γ���