��Ŀ����
����Ŀ����֪����ͼ������������y=ax��ͼ���뷴��������![]() ��ͼ���ڵ�A��3,2����
��ͼ���ڵ�A��3,2����
��1���������������뷴���������ı���ʽ��
��2������ͼ��ֱ��д���ڵ�һ�����ڣ�![]() ��x��ȡֵ��Χ��
��x��ȡֵ��Χ��
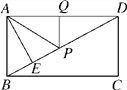
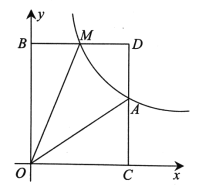
��3��M��m��n���Ƿ���������ͼ���ϵ�һ�����㣬����0��m��3������M��ֱ��MB��x�ᣬ��y���ڵ�B������A��ֱ��AC��y�ύx���ڵ�C����ֱ��MB�ڵ�D�����ı���OADM�����Ϊ6ʱ��֤��BM=DM.
���𰸡���1����������������ʽΪy��![]() x����������������ʽΪ
x����������������ʽΪ![]() ��2��0��x��3��3��������
��2��0��x��3��3��������
��������
��1����A������ֱ��������������ʽ�����a��k��ֵ��������������Ľ���ʽ��
��2���ɷ�����������ͼ��������������ͼ����·�����ö�Ӧ��x��ȡֵ��Χ��
��3����M�������ɱ�ʾ����OCDB������͡�OBM��������Ӷ��ɱ�ʾ���ı���OADM��������ɵõ����̣������M������꣬�Ӷ���֤�����ۣ�
��1��������������y��ax��ͼ���뷴��������![]() ��ͼ���ڵ�A��3��2����
��ͼ���ڵ�A��3��2����
��2��3a��2��![]() �����a��
�����a��![]() ��k��6��
��k��6��
����������������ʽΪy��![]() x����������������ʽΪ
x����������������ʽΪ![]() ��
��
��2����ͼ���֪��������ͼ����ֱ��CD�����ʱ��������������ͼ��������������ͼ����Ϸ���
��A��3��2����
�൱0��x��3ʱ��������������ֵ����������������ֵ��
��3���������֪�ı���OCDBΪ���Σ�
��M��m��n����A��3��2����
��OB��n��BM��m��OC��3��AC��2��
��S����OCBD��OCOB��3n��S��OBM��![]() OBBM��
OBBM��![]() mn��S��OCA��
mn��S��OCA��![]() OCAC��3��
OCAC��3��
��S�ı���OADM��S����OCBDS��OBMS��OCA��3n![]() mn3��
mn3��
���ı���OADM�����Ϊ6ʱ������3n![]() mn3��6��
mn3��6��
�֡�M���ڷ���������ͼ���ϣ�
��mn��6��
��3n��12�����n��4����m��![]() ��
��
��BD��OA��3��
��MΪBD�е㣬
��BM��DM��

 �żӾ���ϵ�д�
�żӾ���ϵ�д�