题目内容
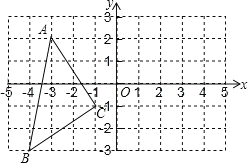
【题目】已知抛物线y=ax2+（2﹣a）x﹣2（a＞0）的图象与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C．给出下列结论：
①在a＞0的条件下，无论a取何值，点A是一个定点；
②在a＞0的条件下，无论a取何值，抛物线的对称轴一定位于y轴的左侧；
③y的最小值不大于﹣2；
④若AB=AC，则a=
．
其中正确的结论有（ ）个．
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
①利用抛物线两点式方程进行判断；
②根据根的判别式来确定a的取值范围，然后根据对称轴方程进行计算；
③利用顶点坐标公式进行解答；
④利用两点间的距离公式进行解答．
①y=ax2+（2-a）x-2=（x-1）（ax+2）．则该抛物线恒过点A（1，0）．故①正确；
②∵y=ax2+（2-a）x-2（a＞0）的图象与x轴有2个交点，
∴△=（2-a）2+8a=（a+2）2＞0，
∴a≠-2．
∴该抛物线的对称轴为：x=
，无法判定的正负．
故②不一定正确；
③根据抛物线与y轴交于（0，-2）可知，y的最小值不大于-2，故③正确；
④∵A（1，0），B（-
，0），C（0，-2），
∴当AB=AC时，
，
解得：a=
,故④正确．
综上所述，正确的结论有3个．
故选：C．
练习册系列答案
相关题目
