Question

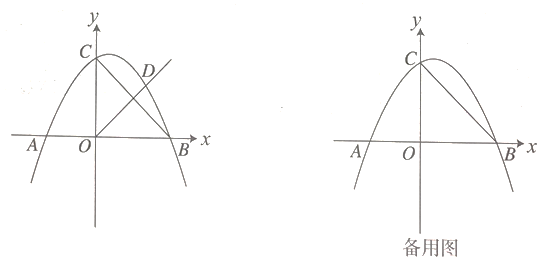
【题目】已知抛物线过点，，．

（1）求此抛物线的解析式；

（2）若点是该抛物线第三象限的任意一点，求四边形的最大面积；

（3）若点在轴上，点为该抛物线的顶点，且，求点的坐标．

Answer 1

【答案】（1）；（2）；（3）(0,)或(0,-)

【解析】

（1）把，，代入解析式，解方程组求出a、b、c，即可求出函数解析式；

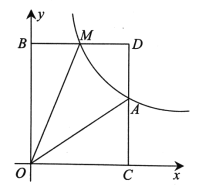
（2）如图1，过点H作HM⊥AB于M，设点H的坐标为：,根据S四边形OCHA=S△AHM+S梯形OCHM=代入整理，得出S四边形OCHA=,再求出二次函数的最大值即可；

（3）假设对称轴与x轴交于N点，根据已知条件可知，NG=NA，以N为圆心NG为半径作圆，与y轴的交点就是Q，再求出它的坐标，然后证明符合条件Q有且只有这两点，即可得出答案．

解：（1）∵抛物线过点，，

∴

解得：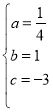

∴抛物线的解析式为：

（2）如图1，过点H作HM⊥AB于M，
设点H的坐标为：（m，），
则HM＝，OM＝-m，
∵点C的坐标为（0，-3），点A的坐标为（-6，0），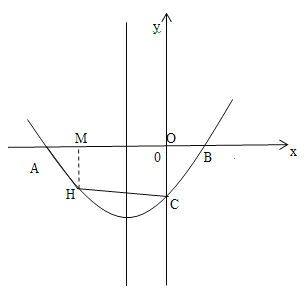

∴OA＝6，OC3，
∴AM＝m +6，
∴S四边形OCHA
＝S△AMH＋S梯形OMHC
＝

=

=

=

∵

∴当m=-3时，S四边形OCHA有最大值
故答案为：S四边形OCHA有最大值，最大面积是；

（3）如图2， ∵，

∴顶点坐标为(-2,-4)，对称轴与x轴交于点N，

∴AN=

∴NG=AN=4

以N为圆心NG为半径作圆，经过点A、B，与y轴交于点Q1、Q2，连接Q1G、Q1A、Q1N，

∵∠ANG=90°且同弧所对的圆周角等于圆心角的一半

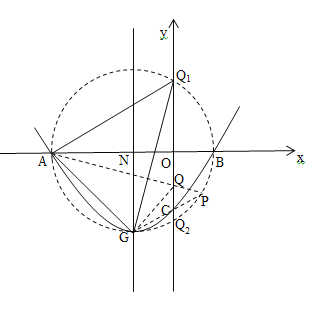
∴∠AQ1G=∠ANG=45°

在Rt△ONQ1中，ON=2，Q1N=4

∴OQ1=

∴Q1 (0,)

由于点Q1、Q2关于 x轴对称，则Q2(0,-)

假设在线段Q1Q2之间有点Q，如图，延长AQ交⊙N于点P，

∴∠APG=∠AQ1G=45°

而∠AQG＞∠APG

∴∠AQG＞45°

∴Q点不在线段Q1Q2之间；

若Q在线段Q1Q2之外时，同理可得∠AQG＜45°

∴点Q不在线段Q1Q2之外；

综上所述，满足条件的点Q的坐标为：(0,)或(0,-)