题目内容
【题目】我们知道,在等腰直角三角形中,底边与一边腰长比为![]() .如图1,
.如图1,![]() ,
,![]() ,则
,则![]() .
.

知识应用:
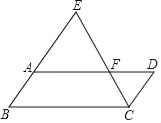
(1)如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,![]() ,
,![]() ,
,![]() 三点共线,若
三点共线,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
知识外延:
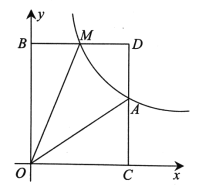
(2)如图3,正方形![]() 中,
中,![]() 和
和![]() 关于
关于![]() 对称,
对称,![]() 点的对应点为
点的对应点为![]() 点,
点,![]() 交
交![]() 的延长线于
的延长线于![]() 点,连接
点,连接![]() .
.
①求证:![]() ;
;
②若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)4;(2)①见解析;②![]()
【解析】
(1)利用SAS证明△ADB≌△AEC,得到BD=EC=2,根据等腰直角三角形底边与一边腰长比求出DE=2,由此得到CD=4;
(2)①证明:根据BC=BE及正方形的性质得到BA=BC=BE,![]() ,从而得到
,从而得到![]() ,故∠FEC
,故∠FEC![]() ,根据FE=FC得到∠FCE
,根据FE=FC得到∠FCE![]() ,
,![]() ,由G为EC的中点得到结论;
,由G为EC的中点得到结论;
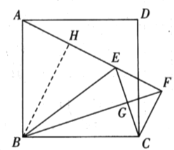
②如图,作![]() ,垂足为
,垂足为![]() ,根据等腰三角形的性质得到HE=1,由
,根据等腰三角形的性质得到HE=1,由![]() 得到EF=1,由此得到HF=2,由
得到EF=1,由此得到HF=2,由![]() 即可求出BF.
即可求出BF.
解:(1) ![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() =2.
=2.
![]() ,
,
![]() ,
,
![]() ;
;
(2)①证明:![]() ,四边形
,四边形![]() 为正方形,
为正方形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
又![]() 为
为![]() 中点,
中点,
![]() ;
;
②解:如图,作![]() ,垂足为
,垂足为![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目