题目内容
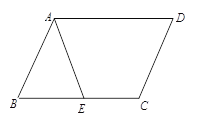
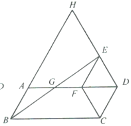
【题目】如图,以平行四边形ABCD的较短边CD为一边作菱形CDEF,使点F落在边AD上,连接BE,交AF于点G,延长DE,BA交于点H,若∠ADC=60°,则![]() =________
=________
【答案】![]()
【解析】
证明△BAG≌△EFG可得AG=GF,设AG=a,CD=b,则DF=AB=b,分别表示BH和DG的长,代入计算即可;
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵四边形CFED是菱形,
∴EF=CD,EF∥CD,
∴AB=EF,AB∥EF,
∴∠GAB=∠GFE,
∵∠AGB=∠FGE,
∴△BAG≌△EFG,
∴AG=GF
∵四边形CFED是菱形,∠ADC=60°
∴CD=CF,△CDF是等边三角形
∴DF=CD
设AG=a,CD=b,则DF=AB=b,
∴FG=AG=a,
∵CD∥BH,
∴∠HAD=∠ADC=60°,
∵∠ADE=60°,
∴∠AHD=∠HAD=∠ADE=60°,
∴△ADH是等边三角形,
∴AD=AH=2a+b,
∴![]()
故答案为:![]()

练习册系列答案
相关题目