题目内容
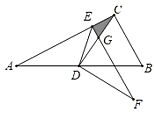
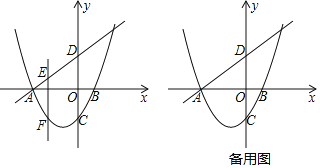
【题目】如图,抛物线y=ax2+bx﹣1(a≠0)交x轴于A,B(1,0)两点,交y轴于点C,一次函数y=x+3的图象交坐标轴于A,D两点,E为直线AD上一点,作EF⊥x轴,交抛物线于点F
(1)求抛物线的解析式;
(2)若点F位于直线AD的下方,请问线段EF是否有最大值?若有,求出最大值并求出点E的坐标;若没有,请说明理由;
(3)在平面直角坐标系内存在点G,使得G,E,D,C为顶点的四边形为菱形,请直接写出点G的坐标.
【答案】(1)抛物线的解析式为y=![]() x 2+
x 2+![]() x﹣1;(2)
x﹣1;(2)![]() ,(
,(![]() ,
,![]() );(3)点G的坐标为(2,1),(﹣2
);(3)点G的坐标为(2,1),(﹣2![]() ,﹣2
,﹣2![]() ﹣1),(2
﹣1),(2![]() ,2
,2![]() ﹣1),(﹣4,3).
﹣1),(﹣4,3).
【解析】
(1)利用待定系数法确定函数关系式;
(2)由函数图象上点的坐标特征:可设点E的坐标为(m,m+3),点F的坐标为(m, ![]() m2+
m2+![]() m﹣1),由此得到EF=﹣
m﹣1),由此得到EF=﹣![]() m2+
m2+![]() m+4,根据二次函数最值的求法解答即可;
m+4,根据二次函数最值的求法解答即可;
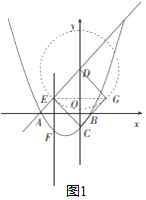
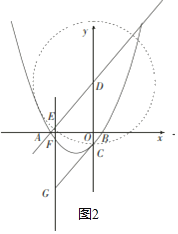
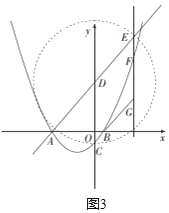
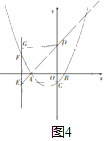
(3)分三种情形①如图1中,当EG为菱形对角线时.②如图2、3中,当EC为菱形的对角线时,③如图4中,当ED为菱形的对角线时,分别求解即可.
(1)将y=0代入y=x+3,得x=﹣3.
∴点A的坐标为(﹣3,0).
设抛物线的解析式为y=a(x﹣x 1)(x﹣x 2),点A的坐标为(﹣3,0),点B的坐标为(1,0),
∴y=a(x+3)(x﹣1).
∵点C的坐标为(0,﹣1),
∴﹣3a=﹣1,得a=![]() ,
,
∴抛物线的解析式为y=![]() x 2+
x 2+![]() x﹣1;
x﹣1;
(2)设点E的坐标为(m,m+3),线段EF的长度为y,
则点F的坐标为(m,![]() m 2+
m 2+![]() m﹣1)
m﹣1)
∴y=(m+3)﹣( ![]() m 2+
m 2+![]() m﹣1)=﹣
m﹣1)=﹣![]() m 2+
m 2+![]() m+4
m+4
即y=-![]() (m﹣
(m﹣![]() ) 2+
) 2+![]() ,
,
此时点E的坐标为(![]() ,
,![]() );
);
(3)点G的坐标为(2,1),(﹣2![]() ,﹣2
,﹣2![]() ﹣1),(2
﹣1),(2![]() ,2
,2![]() ﹣1),(﹣4,3).
﹣1),(﹣4,3).
理由:①如图1,当四边形CGDE为菱形时.
∴EG垂直平分CD
∴点E的纵坐标y=![]() =1,
=1,
将y=1带入y=x+3,得x=﹣2.
∵EG关于y轴对称,
∴点G的坐标为(2,1);
②如图2,当四边形CDEG为菱形时,以点D为圆心,DC的长为半径作圆,交AD于点E,可得DC=DE,构造菱形CDEG
设点E的坐标为(n,n+3),
点D的坐标为(0,3)
∴DE=![]() =
=![]()
∵DE=DC=4,
∴![]() =4,解得n1=﹣2
=4,解得n1=﹣2![]() ,n2=2
,n2=2![]() .
.
∴点E的坐标为(﹣2![]() ,﹣2
,﹣2![]() +3)或(2
+3)或(2![]() ,2
,2![]() +3)
+3)
将点E向下平移4个单位长度可得点G,
点G的坐标为(﹣2![]() ,﹣2
,﹣2![]() ﹣1)(如图2)或(2
﹣1)(如图2)或(2![]() ,2
,2![]() ﹣1)(如图3)
﹣1)(如图3)
③如图4,“四边形CDGE为菱形时,以点C为圆心,以CD的长为半径作圆,交直线AD于点E,
设点E的坐标为(k,k+3),点C的坐标为(0,﹣1).
∴EC=![]() =
=![]() .
.
∵EC=CD=4,
∴2k2+8k+16=16,
解得k1=0(舍去),k2=﹣4.
∴点E的坐标为(﹣4,﹣1)
将点E上移1个单位长度得点G.
∴点G的坐标为(﹣4,3).
综上所述,点G的坐标为(2,1),(﹣2![]() ,﹣2
,﹣2![]() ﹣1),(2
﹣1),(2![]() ,2
,2![]() ﹣1),(﹣4,3).
﹣1),(﹣4,3).

 名校课堂系列答案
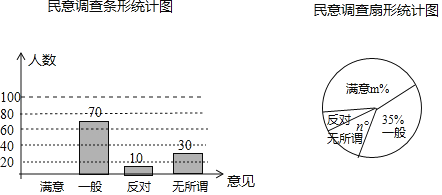
名校课堂系列答案【题目】某校九年级共有400名学生,男女生人数大致相同,调查小组为调查学生的体质健康水平,开展了一次调查研究,将下面的过程补全.
收集数据:
调查小组选取40名学生的体质健康测试成绩作为样本,数据如下:
77 83 80 64 86 90 75 92 83 81
85 86 88 62 65 86 97 96 82 73
86 84 89 86 92 73 57 77 87 82
91 81 86 71 53 72 90 76 68 78
整理、描述数据:
2018年九年级部分学生学生的体质健康测试成绩统计表
成绩 | 50≤x<55 | 55≤x<60 | 60≤x<65 | 65≤x<70 | 70≤x<75 |
人数 | 1 | 1 | 2 | 2 | 4 |
成绩 | 75≤x<80 | 80≤x<85 | 85≤x<90 | 90≤x<95 | 95≤x<100 |
人数 | 5 | a | b | 5 | 2 |
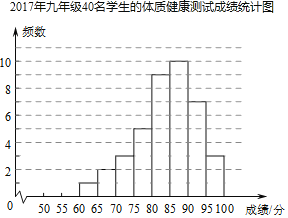
分析数据:
(1)写出表中的a、b的值;
(2)分析上面的统计图、表,你认为学生的体重健康测试成绩是2017年还是2018年的好?说明你的理由.(至少写出两条).
(3)体育老师根据2018年的统计数据,安排80分以下的学生进行体育锻炼,那么全年级大约有多少人参加?
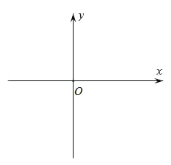
【题目】已知二次函数y=x2﹣2x﹣1.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
(1)请在表内的空格中填入适当的数;
(2)根据列表,请在所给的平面直角坐标系中画出y=x2﹣2x﹣1的图象;
(3)当x在什么范围内时,y随x增大而减小;