题目内容
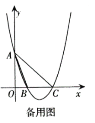
【题目】在△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC有公共点E,连结DE并延长,与BC的延长线交于点F ,BD=BF.
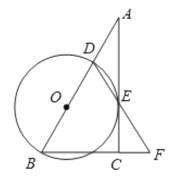
(1)求证:AC是⊙O的切线;
(2)若∠F=60°,BF=8,求CF的长.
【答案】(1)详见解析;(2)CF=2.
【解析】
(1)连接连接BE,OE,根据直径所对的角为直角结合等腰三角形三线合一的性质可证得DE=EF,根据三角形中位线定理可推出OE∥BC,得出OE⊥AC,即可证明结论;
(2)利用三角形中位线定理可求得半径OE的长,利用含30度角的直角三角形的性质可求得OA进而求得AB,即可求得BC的长,从而得解.
(1)连接BE,OE,
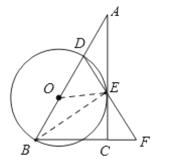
∵BD是直径,
∴∠DEB=90°,
∴BE⊥DF,
∵BD=BF,
∴DE=EF,
又∵DO=OB,
∴OE∥BF,
∵∠ACB=90°,
∴∠OEA=∠ACB =90°,
∴OE⊥AC,
∴AC是圆O的切线;
(2)∵BD=BF,∠F=60°,
∴△DBF为等边三角形,
∴∠ABC=60°,
∴∠A=∠ACB-∠ABC =90°-60°=30°,
∵DE=EF,DO=OB,
∴OE=![]() ,
,
在![]() 中,∠OEA =90°,∠A=30°,
中,∠OEA =90°,∠A=30°,
∴AO=2OE=8,
∴AB= AO +OB= AO +OE= 8 +4=12,
在![]() 中,∠ACB =90°,∠A=30°,
中,∠ACB =90°,∠A=30°,
∴BC=![]() =6,
=6,
∴CF=BF-BC=2.

练习册系列答案
相关题目