题目内容
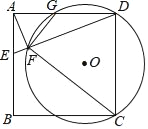
【题目】在平行四边形ABCD中,E为BC边上的一点.连结AE.
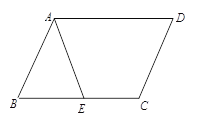
(1)若AB=AE, 求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF︰FA的值.
【答案】(1)详见解析;(2)EF︰FA=1︰2,解题过程见解析.
【解析】
试题(1)由平行四边形的性质可得∠ABC=∠ADC;由平行线的性质可得∠AEB=∠EAD;由等腰三角形的性质可得∠ABC=∠AEB;再由等量代换即可得∠EAD=∠ADC;(2)易证△ADF∽△EBF,根据相似三角形对应边的比相等即可得EF︰FA的值.
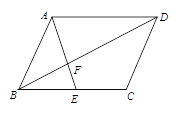
试题解析:(1)证明:∵四边形ABCD为平行四边形,
∴ ∠ABC=∠ADC AD∥BC.
∴∠AEB=∠EAD.
又∵AE=AB
∴∠ABC=∠AEB.
∴∠ABC=∠EAD.
∴∠EAD=∠ADC.
(2)∵AD∥BC,
∴∠FAD=∠FEB,∠ADF=∠EBF,
∴△ADF∽△EBF.
EF︰FA= BE︰AD= BE︰ BC=1︰2

练习册系列答案
相关题目