题目内容
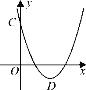
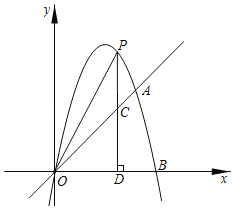
【题目】如图,已知二次函数的图象经过点A(4,4),B(5,0)和原点O,P为二次函数图象上的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA相较于点C.
(1)求出二次函数的解析式;
(2)当点P在直线OA的上方时,求线段PC的最大值;
(3)当点P在直线OA的上方时,是否存在一点P,使射线OP平分∠AOy,若存在,请求出P点坐标;若不存在.请说明理由;
(4)当m>0时,探索是否存在点P,使得△PCO为等腰三角形,若存在,求出P点的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2+5x;(2)4;(3)存在,P(4﹣![]() ,2+3
,2+3![]() );(4)存在,P(4﹣
);(4)存在,P(4﹣![]() ,2+3
,2+3![]() )
)
【解析】
(1)由待定系数法将A(4,4),B(5,0)代入二次函数的解析式为y=ax2+bx即可;
(2)求出OA的解析式,将P,C的纵坐标用含m的代数式表示出来,再表示出PC的长度,用函数的思想即可求出其最大值;
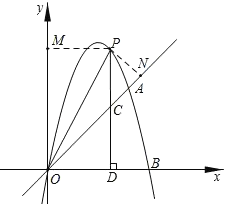
(3)存在,如图,当射线OP平分∠AOy时,过点P作PM⊥y轴于点M,作PN⊥OA于点N,则PM=PN,证△ODC和△PCN是等腰直角三角形,可用含m的代数式分别表示出PM,PN的长度,解等式即可求出m的值,进一步写出点P的坐标;
(4)存在,当△PCO为等腰三角形时,只存在PC=OC一种情况,用含m的代数式表示出PC,OC的长,解方程即可求出m的值,进一步写出点P的坐标.
解:(1)∵二次函数的图象经过原点,
∴设二次函数的解析式为y=ax2+bx,
将A(4,4),B(5,0)代入,
得![]() ,
,
解得,a=﹣1,b=5,
∴y=﹣x2+5x;
(2)设直线OA的解析式为y=ax,
将A(4,4)代入,
得,a=1,
∴yOA=x,
∵PD⊥x轴,D(m,0),
∴P(m,﹣m2+5m),C(m,m),
∴PC=﹣m2+5m﹣m
=﹣m2+4m
=﹣(m﹣2)2+4,
根据二次函数的图象及性质可知,当m=2时,PC有最大值,其最大值为4;
(3)存在,理由如下:
如图,当射线OP平分∠AOy时,过点P作PM⊥y轴于点M,作PN⊥OA于点N,
则PM=PN,
∵点C在直线yOA=x上,
∴△ODC是等腰直角三角形,
∴∠OCD=∠PCN=45°,
∴△PCN是等腰直角三角形,
由(2)知,PC=﹣m2+4m,
∴PN=![]() (﹣m2+4m)=﹣
(﹣m2+4m)=﹣![]() m2+2
m2+2![]() m,
m,
∵P(m,﹣m2+5m),
∴PM=m,
∵PM=PN,
∴m=﹣![]() m2+2
m2+2![]() m,
m,
解得,m1=0(舍去),m2=4﹣![]() ,
,
∴P(4﹣![]() ,2+3
,2+3![]() );
);
(4)存在,理由如下:
∵∠PCO=180°﹣∠OCD=135°,
∴当△PCO为等腰三角形时,只存在PC=OC一种情况,
由(2)知,PC=﹣m2+4m,OC=![]() OD=
OD=![]() m,
m,
∴﹣m2+4m=![]() m,
m,
解得,m1=0(舍去),m2=4﹣![]() ,
,
∴当m=4﹣![]() 时,﹣m2+5m=2+3
时,﹣m2+5m=2+3![]() ,
,
∴P(4﹣![]() ,2+3
,2+3![]() ).
).

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案