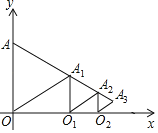
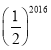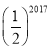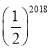题目内容
【题目】如图,在由每个边长为1的小正方形组成的9×9的网格中,点A,B,C都在格点上,点B绕点C逆时针旋转90°后的对应点为M,已知点B的坐标为(0,﹣2)(坐标轴与网格线平行).
(1)直接写出:点C的坐标为 ,点M的坐标为 ;
(2)若平面内存在一点P,且P为△ACM的外心,直接写出点P的坐标是 ;
(3)CN平分∠BCM交y轴于点N,则N点坐标为 .

【答案】(1)(﹣3,2),(1,5);(2)(![]() ,0);(3)(0,
,0);(3)(0,![]() )
)
【解析】
(1)先建立直角坐标系,作出图形,构造全等三角形,即可得出结论;
(2)先判断出PA=PC,再判断出点P的纵坐标为0,利用PA=PM建立方程求解即可得出结论;
(3)利用角平分线的特点构造出等腰三角形求出MF,进而求出直线CF的解析式,即可得出结论.
解:(1)建立如图1所示的平面坐标系,
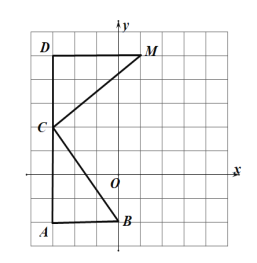
由网格知,A(﹣3,-2),C(﹣3,2),
∴AC⊥x轴,AC=4,
∵B(0,-2),
∴AB=3,
过点M作AC的垂线交AC于D,
∴∠CDM=∠BAC=90°,
∴∠DCM+CMD=90°,
由旋转知,BC=MC,∠BCM=90°,
∴∠ACB+∠DCM=90°,
∴∠ACB=∠DMC,
∴△ABC≌△DCM(AAS),
∴DM=AC=4,CD=AB=3,
∴AD=AC+CD=7.
∴M(1,5),
故答案为(﹣3,2),(1,5);
(2)由(1)知,A(-3,-2),C(﹣3,2),
设点P的坐标为(m,n)
∵点P是△ACM的外接圆的圆心,
∴点P到点A,C,M的距离相等,
由(1)知,A(-3,-2),C(﹣3,2),
∴n=0,
∴P(m,0),
而PA=![]() ,
,![]()
![]()
∴m=![]() ,
,
∴P(![]() ,0),
,0),
故答案为(![]() ,0);
,0);
(3)如图3,
过点M作MF∥AC交CN于F,
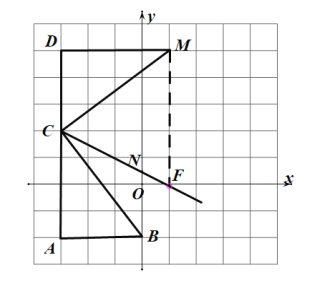
∴∠CFM=∠ACN,
∵CN是∠ACM的角平分线
∴∠ACN=∠MCN,
∴∠MCN=∠CFN,
∴MF=CM,
而CM=![]()
∴MF=5,
∴F(1,0),
∵C(﹣3,2),
设直线CF的解析式为![]() ,
,
将F,C代入得
![]() 解得
解得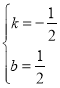
∴直线CF的解析式为![]()
令x=0,则y=![]() ,
,
∴N(![]() ).
).
故答案为(![]() ).
).