Question

【题目】已知二次函数y＝(x－m)2－1.

（1）当二次函数的图象经过坐标原点O(0，0)时，求二次函数的解析式；

（2）如下图，当m＝2时，该抛物线与轴交于点C，顶点为D，求C、D 两点的坐标；

Answer 1

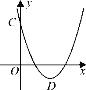
【答案】（1）y＝x2＋2x或y＝x2－2x；（2）C(0，3)，D(2，－1)

【解析】

（1）根据二次函数的图象经过坐标原点O（0，0），直接代入求出m的值即可得二次函数的解析式；
（2）根据m=2，代入求出二次函数解析式，进而利用配方法求出顶点坐标以及图象与y轴交点即可．

解：（1）∵二次函数的图象经过坐标原点O(0，0)，
∴代入二次函数y＝(x－m)2－1得m2－1＝0，得m＝±1，

所以二次函数的解析式为y＝x2＋2x或y＝x2－2x；

（2）当m＝2时，y＝(x－2)2－1，

∴D(2，－1)，

又当x＝0时，y＝3，

∴C(0，3)