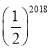题目内容
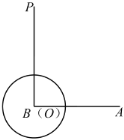
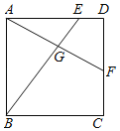
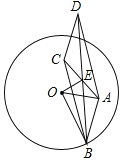
【题目】如图，⊙O的半径为4
，点B是圆上一动点，点A为⊙O内一定点，OA＝4，将AB绕A点顺时针方向旋转120°到AC，以AB、BC为邻边作ABCD，对角线AC、BD交于E，则OE的最大值为_____．
【答案】2
+2
【解析】
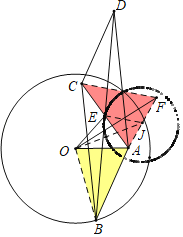
如图，构造等腰△OAF，使得AO＝AF，∠OAF＝120°，连接CF，OB，取AF的中点J，连接EJ．证明EJ是定值，可得点E的运动轨迹是以J为圆心，EJ为半径的圆，由此即可解决问题．
如图，构造等腰△OAF，使得AO＝AF，∠OAF＝120°，连接CF，OB，取AF的中点J，连接EJ．
∵∠BAC＝∠OAF＝120°，
∴∠BAO＝∠CAF，
∵ABAC，AO＝AF，
∴△OAB≌△FAC（SAS），
∴CF＝OB＝
，
∵四边形BCDA是平行四边形，
∴AE＝EC，
∵AJ＝JF，
∴EJ＝
CF＝
，
∴点E的运动轨迹是以J为圆心，EJ为半径的圆，
易知OJ＝
当点E在OJ的延长线上时，OE的值最大，最大值为OJ+JE＝
，
故答案为2+2．
练习册系列答案
名校课堂系列答案
相关题目
