题目内容
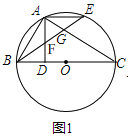
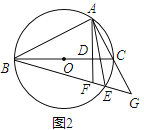
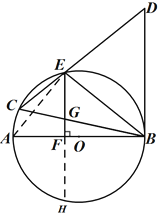
【题目】如图,在⊙![]() 中,AB是直径,BC是弦,BC=BD,连接CD交⊙
中,AB是直径,BC是弦,BC=BD,连接CD交⊙![]() 于点E,∠BCD=∠DBE.
于点E,∠BCD=∠DBE.
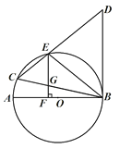
(1)求证:BD是⊙![]() 的切线.
的切线.
(2)过点E作EF⊥AB于F,交BC于G,已知DE=![]() ,EG=3,求BG的长.
,EG=3,求BG的长.
【答案】(1)见解析;(2)BG的长为5.
【解析】
(1)连接AE,根据圆周角定理可得∠BAE=∠BCE,由AB是直径可得∠AEB=90°,进而可得∠BAE+∠ABE=90°,由∠BCD=∠DBE.利用等量代换即可求出∠ABD=90°,可得BD是⊙O的切线;(2)延长EF交⊙O于H,根据垂径定理可得![]() ,进而可得∠ECB=∠BEH,由∠EBC是公共角即可证明△EBC∽△GBE,根据相似三角形的性质可得
,进而可得∠ECB=∠BEH,由∠EBC是公共角即可证明△EBC∽△GBE,根据相似三角形的性质可得![]() ,根据等腰三角形的性质可得∠D=∠BCE,利用等量代换可得∠D=∠DBE,可得BE=DE,由∠AFE=∠ABD=90°可得EF//BD,根据平行线性质可得∠D=∠CEF,即可证明∠BCE=∠CEF,可得CG=GE,即可得出BC=BG+EG,代入
,根据等腰三角形的性质可得∠D=∠BCE,利用等量代换可得∠D=∠DBE,可得BE=DE,由∠AFE=∠ABD=90°可得EF//BD,根据平行线性质可得∠D=∠CEF,即可证明∠BCE=∠CEF,可得CG=GE,即可得出BC=BG+EG,代入![]() 求出BG的长即可.
求出BG的长即可.
(1)如图,连接AE,则∠BAE=∠BCE,
∵AB是直径,
∴∠AEB=90°,
∴∠BAE+∠ABE=90°,
∴∠ABE+∠BCE=90°,
∵∠BCE=∠DBE,
∴∠ABE+∠DBE=90°,即∠ABD=90°,
∴BD是⊙O的切线.
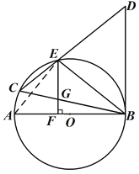
(2)如图,延长EF交⊙O于H,
∵EF⊥AB,AB是直径,
∴![]() ,
,
∴∠ECB=∠BEH,
∵∠EBC=∠GBE,
∴△EBC∽△GBE,
∴![]() ,
,
∵BC=BD,
∴∠D=∠BCE,
∵∠BCE=∠DBE,
∴∠D=∠DBE,
∴BE=DE=![]() ,
,
∵∠AFE=∠ABD=90°,
∴BD∥EF,
∴∠D=∠CEF,
∴∠BCE=∠CEF,
∴CG=GE=3,
∴BC=BG+CG=BG+3,
∴![]() ,
,
∴BG=-8(舍)或BG=5,
即BG的长为5.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案