Question

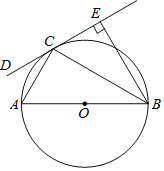
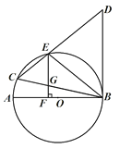
【题目】如图，AE、BE是△ABC的两个内角的平分线，过点A作AD⊥AE．交BE的延长线于点D．若AD＝AB，BE：ED＝1：2，则cos∠ABC＝_____．

Answer 1

【答案】

【解析】

取DE的中点F，连接AF，根据直角三角形斜边中点的性质得出AF＝EF，然后证得△BAF≌△DAE，得出AE＝AF，从而证得△AEF是等边三角形，进一步证得∠ABC＝60°，即可求得结论．

取DE的中点F，连接AF，

∴EF＝DF，

∵BE：ED＝1：2，

∴BE＝EF＝DF，

∴BF＝DE，

∵AB＝AD，

∴∠ABD＝∠D，

∵AD⊥AE，EF＝DF，

∴AF＝EF，

在△BAF和△DAE中

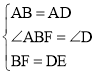
∴△BAF≌△DAE（SAS），

∴AE＝AF，

∴△AEF是等边三角形，

∴∠AED＝60°，

∴∠D＝30°，

∵∠ABC＝2∠ABD，∠ABD＝∠D，

∴∠ABC＝60°，

∴cos∠ABC＝cos60°＝，

故答案为：．